题目内容
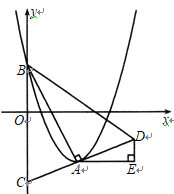
【题目】如图，在平面直角坐标系xOy中，抛物线
的顶点为A，与y轴的交点为B，连接AB，AC⊥AB，交y轴于点C，延长CA到点D，使AD=AC，连接BD，作AE∥x轴，DE∥y轴.
（1）当m=2时，求点B的坐标；
（2）求DE的长；
（3）设点D的坐标为(x，y)，求y关于x的函数关系式.
【答案】（1）（0，2）；（2）4；（3）
.
【解析】试题分析：（1）将m=2代入原式，得到二次函数的顶点式，据此即可求出B点的坐标；
（2）延长EA，交y轴于点F，证出
≌
，进而证出
利用相似三角形的性质，求出
（3）根据点A和点B的坐标，得到
， 
，将
代入
即可求出二次函数的表达式；
试题解析：
（1）当m=2时， 
，
当x=0时，y=2，∴点B的坐标为（0，2）.
（2）延长EA，交y轴于点F， 
， 
，
∴
≌
， 
∵当
时，点
，点
，
∴
，
，
∵
， 
，
∴
∴
，即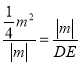
，
∴
（3）∵点A的坐标为
，又∵
∴点D的坐标为
，
∴
， 
，
∴
，
∴所求函数的解析式为
.
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
【题目】下图是某同学在沙滩上用石子摆成的小房子，请根据图中的信息完成下列的问题：
（1）填写下表：
图形编号 | ① | ② | ③ | ④ | …… |
图中石子的总数 | …… |
（2）第30个图形需要用 颗石子；
（3）如果继续摆放下去，那么第
个图案要用 颗石子；
（4）该同学准备用300颗石子来摆放第个图案，摆放成完整的图案后，第个图案 能否刚好用完这300颗石子？如果可以，求出的值，如果不能，求出的最大值以及至少还剩余多少颗石子．
