题目内容
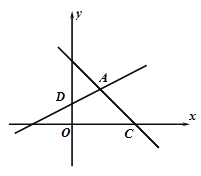
【题目】在平面直角坐标系xOy中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y = x上,那么称该菱形为点A,C的“极好菱形”. 下图为点A,C的“极好菱形”的一个示意图.
已知点M的坐标为(1,1),点P的坐标为(3,3).
(1)点E(2,1),F(1,3),G(4,0)中,能够成为点M,P的“极好菱形”的顶点的是 ;
(2)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;

②当四边形MNPQ的面积为8,且与直线y = x + b有公共点时,写出b的取值范围.
【答案】(1)F,G(2)①4②![]() .
.
【解析】试题分析:(1)根据“极好菱形”的定义即可判定;(2)①四边形MNPQ是点M,P的“极好菱形”,当点N的坐标为(3,1)时,可得四边形MNPQ是正方形,即可得四边形MNPQ的面积;②根据菱形的面积公式求得菱形另一条对角线的长,再由y = x + b有公共点,即可得结论.
试题解析:
(1)F,G.
(2)①∵M(1,1),P(3,3),N(3,1),∴![]() ,
,![]() .
.
∵四边形MNPQ是菱形,∴四边形MNPQ是正方形.
∴![]() .
.
②![]() .
.

练习册系列答案
相关题目