Question

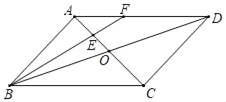
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转得到正方形此时,点落在对角线AC上,点落在CD的延长线上,交AD于点E,连接、CE．

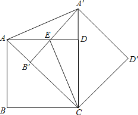
求证：(1)≌；

(2)直线CE是线段的垂直平分线．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）根据正方形的性质可得AD=CD，∠ADC=90°，∠EA′D=45°，则∠A′DE=90°，再计算出∠A′ED=45°，根据等角对等边可得A′D=ED，即可利用SAS证明△ADA′≌△CDE；
（2）利用等腰三角形三线合一的性质即可证明．

四边形ABCD是正方形,

∴AD=CD，∠ADC=90°，
∴∠A′DE=90°，
根据旋转的方法可得：∠EA′D=45°，
∴∠A′ED=45°，
∴A′D=ED，

在和中,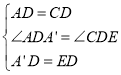

≌；

由正方形的性质及旋转,得,又,

在 和中

≌

,

是等腰三角形

∴直线CE是线段的垂直平分线（等腰三角形三线合一）．