题目内容
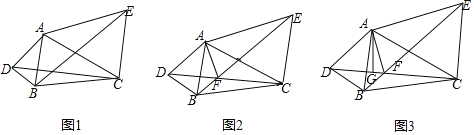
【题目】如图,△ABD和△ACE中,AB=AD,AC=AE,∠DAB=∠CAE=α,连接DC、BE.
(1)如图1,求证:DC=BE;
(2)如图2,DC,BE交于点F,用含α的式子表示∠AFE;
(3)如图3,过A作AG⊥DC于点G,式于![]() 的值为 .
的值为 .
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由∠DAB=∠CAE=α,可得∠DAC=∠BAE,根据“SAS”可证△ADC≌△ABE,可得DC=BE;
(2)由△ADC≌△ABE可得∠AEF=∠ACD,即可证点A,点E,点C,点F四点共圆,可得∠AFE=∠ACE,根据等腰三角形的性质和三角形内角和定理可求∠AFE的度数;
(3)由题意可得∠AFD=![]() =∠AFE,过点作AH⊥BE,可证△AGF≌△AHF,可得AG=AH,GF=HF,即可证Rt△AGC≌Rt△AHE,可得GC=HE,由EF﹣FC=HE+FH﹣FC=GC+FH﹣FC=GF+FC+FH﹣FC=2GF,可得
=∠AFE,过点作AH⊥BE,可证△AGF≌△AHF,可得AG=AH,GF=HF,即可证Rt△AGC≌Rt△AHE,可得GC=HE,由EF﹣FC=HE+FH﹣FC=GC+FH﹣FC=GF+FC+FH﹣FC=2GF,可得![]() 的值.
的值.
(1)∵∠DAB=∠CAE=α,
∴∠DAB+∠BAC=∠CAE+∠BAC
即∠DAC=∠BAE,
又∵AD=AB,AC=AE
∴△ADC≌△ABE(SAS)
∴DC=BE
(2)∵△ADC≌△ABE
∴∠AEF=∠ACD
∴点A,点E,点C,点F四点共圆
∴∠AFE=∠ACE
∵AC=AE,∠DAB=∠CAE=α
∴∠ACE=![]()
∴∠AFE=![]()
(3)∵△ADC≌△ABE
∴∠ADC=∠ABE
∴点A,点D,点B,点F四点共圆
∴∠AFD=∠ABD
∵AB=AD,∠DAB=∠CAE=α
∴∠ABD=![]()
∴∠AFD=![]()
∴∠AFE=∠AFD
如图,过点作AH⊥BE,

∵∠AFE=∠AFD,∠AGF=∠AHF,AF=AF
∴△AGF≌△AHF(AAS)
∴AG=AH,GF=HF,
∵AG=AH,AE=AC
∴Rt△AGC≌Rt△AHE(HL)
∴GC=HE
∵EF﹣FC=HE+FH﹣FC=GC+FH﹣FC=GF+FC+FH﹣FC=2GF,
∴![]() =
=![]() =
=![]()
故答案为:![]()



