题目内容
【题目】如图,⊙O的直径AD长为6,AB是弦,CD∥AB,∠A=30°,且CD=![]() .
.
(1)求∠C的度数;
(2)求证:BC是⊙O的切线.
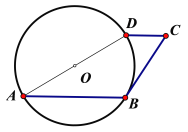
【答案】(1)60°;(2)见解析
【解析】
(1)连接BD,由AD为圆的直径,得到∠ABD为直角,再利用30度角所对的直角边等于斜边的一半求出BD的长,根据CD与AB平行,得到一对内错角相等,确定出∠CDB为直角,在直角三角形BCD中,利用锐角三角函数定义求出tanC的值,即可确定出∠C的度数;
(2)连接OB,由OA=OB,利用等边对等角得到一对角相等,再由CD与AB平行,得到一对同旁内角互补,求出∠ABC度数,由∠ABC﹣∠ABO度数确定出∠OBC度数为90,即可得证;
(1)如图,连接BD,
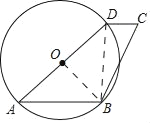
∵AD为圆O的直径,
∴∠ABD=90°,
∴BD=![]() AD=3,
AD=3,
∵CD∥AB,∠ABD=90°,
∴∠CDB=∠ABD=90°,
在Rt△CDB中,tanC=![]() ,
,
∴∠C=60°;
(2)连接OB,
∵∠A=30°,OA=OB,
∴∠OBA=∠A=30°,
∵CD∥AB,∠C=60°,
∴∠ABC=180°﹣∠C=120°,
∴∠OBC=∠ABC﹣∠ABO=120°﹣30°=90°,
∴OB⊥BC,
∴BC为圆O的切线.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目