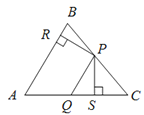
题目内容
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若AQ
AB,若AQ![]() PQ,PR
PQ,PR![]() PS,则下列结论:①AS
PS,则下列结论:①AS![]() AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=
AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=![]() .其中正确的结论有____________(填序号).
.其中正确的结论有____________(填序号).
【答案】①②
【解析】连接AP.

∵PR=PS,AP=AP,PR⊥AB,PS⊥AC,
∴△APR≌△APS,
∴AS=AR,①正确.
∵PR=PS,PR⊥AB,PS⊥AC,
∴AP是∠BAC的平分线,
∴∠BAP=∠QAP.
∵AQ=PQ,
∴∠QAP=∠QPA,
∴∠BAP=∠QPA,
∴QP∥AR,②正确.
点P是BC的上的点,并没有固定,明显△BRP≌△CSP不成立,故③不正确;
∵![]()
![]()
根据已知条件不能得出AR+AQ=![]() (AB+AC),故④错误;故答案为:①②.
(AB+AC),故④错误;故答案为:①②.

练习册系列答案
相关题目





