题目内容
【题目】如图,抛物线![]() 经过原点,与
经过原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,将抛物线
,将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
, ![]() 交
交![]() 轴于
轴于![]() ,
, ![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴于点
轴于点![]() .
.


(![]() )求抛物线
)求抛物线![]() 的解析式及顶点坐标.
的解析式及顶点坐标.
(![]() )以
)以![]() 为斜边向上作等腰直角三角形
为斜边向上作等腰直角三角形![]() ,当点
,当点![]() 落在抛物线
落在抛物线![]() 的对称轴上时,求抛物线
的对称轴上时,求抛物线![]() 的解析式.
的解析式.
(![]() )若抛物线
)若抛物线![]() 的对称轴存在点
的对称轴存在点![]() ,使
,使![]() 为等边三角形,请直接写出
为等边三角形,请直接写出![]() 的值.
的值.
【答案】(1)抛物线![]() 的解析式为
的解析式为![]() ,顶点坐标
,顶点坐标![]() ;
;
(2)抛物线![]() 的解析式为:
的解析式为: ![]() ;
;
(3)![]() .
.
【解析】试题分析:(1)把(0,0)及(2,0)代入y=x2+bx+c,求出抛物线C1的解析式,即可求出抛物线C1的顶点坐标;
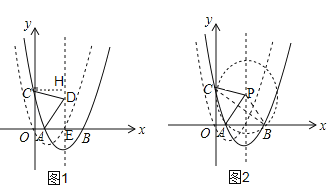
(2)先求出C2的解析式,确定A,B,C的坐标,过点C作CH⊥对称轴DE,垂足为H,利用△PAC为等腰直角三角形,求出角的关系可证得△CHD≌△DEA,再由OC=EH列出方程求解得出m的值,即可得出C2的解析式.
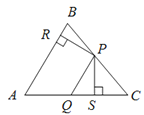
(3)连接BC,BP,由抛物线对称性可知AP=BP,由△PAC为等边三角形,可得AP=BP=CP,∠APC=60°,由C,A,B三点在以点P为圆心,PA为半径的圆上,可得BC=2OC,利用勾股定理求出OB=![]() OC,列出方程求出m的值即可.
OC,列出方程求出m的值即可.
试题解析:解:(1)∵抛物线C1经过原点,与x轴的另一个交点为(2,0),∴![]() ,解得:
,解得: ![]() ,∴抛物线C1的解析式为y=x2﹣2x,∴抛物线C1的顶点坐标(1,﹣1);
,∴抛物线C1的解析式为y=x2﹣2x,∴抛物线C1的顶点坐标(1,﹣1);
(2)如图1,∵抛物线C1向右平移m(m>0)个单位得到抛物线C2,∴C2的解析式为y=(x﹣m﹣1)2﹣1,∴A(m,0),B(m+2,0),C(0,m2+2m),过点C作CH⊥对称轴DE,垂足为H,∵△ACD为等腰直角三角形,∴AD=CD,∠ADC=90°,∴∠CDH+∠ADE=90°,∴∠HCD=∠ADE,∵∠DEA=90°,∴△CHD≌△DEA,∴AE=HD=1,CH=DE=m+1,∴EH=HD+DE=1+m+1=m+2,由OC=EH得m2+2m=m+2,解得m1=1,m2=﹣2(舍去),∴抛物线C2的解析式为:y=(x﹣2)2﹣1.
(3)如图2,连接BC,BP,由抛物线对称性可知AP=BP,∵△PAC为等边三角形,∴AP=BP=CP,∠APC=60°,∴C,A,B三点在以点P为圆心,PA为半径的圆上,∴∠CBO=![]() ∠CPA=30°,∴BC=2OC,∴由勾股定理得OB=
∠CPA=30°,∴BC=2OC,∴由勾股定理得OB=![]() =
=![]() OC,∴
OC,∴![]() (m2+2m)=m+2,解得m1=
(m2+2m)=m+2,解得m1=![]() ,m2=﹣2(舍去),∴m=
,m2=﹣2(舍去),∴m=![]() .
.