题目内容
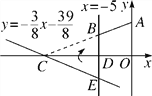
【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-![]() x-
x-![]() 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
【答案】(1)C(-13,0),E(-5,-3), y=![]() x+5;(2)32;(3)答案见解析
x+5;(2)32;(3)答案见解析
【解析】试题分析:
(1)在y=-![]() x-
x-![]() 中,由y=0解得对应的x的值即可得到点C的坐标;在y=-
中,由y=0解得对应的x的值即可得到点C的坐标;在y=-![]() x-
x-![]() 中,由x=-5求得对应的y的值即可得到点E的坐标,结合点B和点E关于x轴对称可得点B的坐标,结合点A的坐标即可求得直线AB的解析式;
中,由x=-5求得对应的y的值即可得到点E的坐标,结合点B和点E关于x轴对称可得点B的坐标,结合点A的坐标即可求得直线AB的解析式;
(2)由点C、E、B、A的坐标结合图形分别求出△CDE和四边形ABDO的面积相加即可得到S的值;
(3)由已知条件计算出△AOC的面积与(2)中结果对比即可说明他的说法是错误的,理由是由(1)可知AB的解析式为y=![]() x+5,将点C的坐标代入检验,即可发现点C不在直线AB上,由此可知他的计算方法是错误的.
x+5,将点C的坐标代入检验,即可发现点C不在直线AB上,由此可知他的计算方法是错误的.
试题解析:
(1)在直线y=-![]() x-
x-![]() 中,
中,
令y=0,则有0=-![]() x-
x-![]() ,
,
∴x=-13,
∴C(-13,0).
令x=-5,
则有y=-![]() ×(-5)-
×(-5)-![]() =-3,
=-3,
∴E(-5,-3).
∵点B,E关于x轴对称,
∴B(-5,3).
∵A(0,5),
∴设直线AB的解析式为y=kx+5,
∴-5k+5=3,
∴k=![]() ,
,
∴直线AB的解析式为y=![]() x+5.
x+5.
(2)由(1)知E(-5,-3),
∴DE=3.
∵C(-13,0),
∴CD=-5-(-13)=8,
∴S△CDE=![]() CD·DE=12.
CD·DE=12.
由题意知OA=5,OD=5,BD=3,
∴S四边形ABDO=![]() (BD+OA)·OD=20,
(BD+OA)·OD=20,
∴S=S△CDE+S四边形ABDO=12+20=32.
(3)由(2)知S=32,在△AOC中,OA=5,OC=13,
∴S△AOC=![]() OA·OC=
OA·OC=![]() =32.5,
=32.5,
∴S≠S△AOC.
理由:由(1)知直线AB的解析式为y=![]() x+5,
x+5,
令y=0,则0=![]() x+5,
x+5,
∴x=-![]() ≠-13,
≠-13,
∴点C不在直线AB上,即点A,B,C不在同一条直线上,
∴S△AOC≠S.

【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm