题目内容
【题目】把![]() 和
和![]() 按如图
按如图![]() 摆放(点
摆放(点![]() 与
与![]() 重合),点
重合),点![]() 、
、![]() 、
、![]() 在同一条直线上.已知:
在同一条直线上.已知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如图
.如图![]() ,
,![]() 从图
从图![]() 的位置出发,以
的位置出发,以![]() 的速度沿
的速度沿![]() 向
向![]() 匀速移动,在
匀速移动,在![]() 移动的同时,点
移动的同时,点![]() 从
从![]() 的顶点
的顶点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动;当点
匀速移动;当点![]() 移动到点
移动到点![]() 时,点
时,点![]() 停止移动,
停止移动,![]() 也随之停止移动.
也随之停止移动.![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,设移动时间为
,设移动时间为![]() .
.
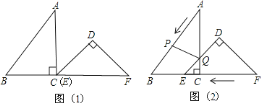
![]() 用含
用含![]() 的代数式表示线段
的代数式表示线段![]() 和
和![]() 的长,并写出
的长,并写出![]() 的取值范围;
的取值范围;
![]() 当
当![]() 为何值时,
为何值时,![]() 是等腰三角形.
是等腰三角形.
【答案】![]()
![]() 的取值范围是:
的取值范围是:![]() ;
;![]() 当
当![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形
是等腰三角形
【解析】
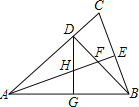
(1)根据题意以及直角三角形性质,表达出CQ、AQ,再根据当点P移动到点B时,点P停止移动,得出t的取值范围;
(2)分三种情况进行讨论:①若AP=AQ;②若AP=PQ;③若AQ=PQ,根据题意以及相似三角形对应边成比例,列出比例式进行计算即可得出结论.
![]() 解:∵点
解:∵点![]() 从
从![]() 的顶点
的顶点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速移动,
匀速移动,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵当点![]() 移动到点
移动到点![]() 时,点
时,点![]() 停止移动,
停止移动,
∴![]() 的取值范围是:
的取值范围是:![]() ;
;![]() 解:分三种情况:
解:分三种情况:
①若![]() ,则有
,则有![]() ,如图
,如图![]() ,
,
解得:![]() ;
;
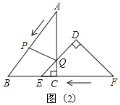
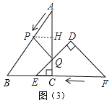
②若![]() ,如图
,如图![]() ,过点
,过点![]() 作
作![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() ;
;
③若![]() ,如图
,如图![]() ,过点
,过点![]() 作
作![]() ,则
,则![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]()
综上所述,当![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
相关题目