题目内容
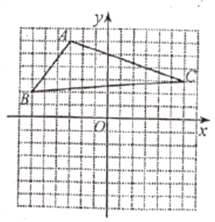
【题目】如图,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() ,垂足为
,垂足为![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.

(1)若![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)100;(2)见解析.
【解析】
(1)先证明四边形ABCD是正方形,再根据已知条件证明△BCF≌△DCE,即可得到四边形![]() 的面积=正方形ABCD的面积;
的面积=正方形ABCD的面积;
(2) 延长BG交AD于点M,作AN⊥MN,连接FG,先证明四边形BCEM是平行四边形,得到BM=CE,证明△BCF≌△GCF,得到BF=GF,∠FGC=∠FBC=![]() ,由AN⊥MN,得GM=2MN,根据∠BAC=45
,由AN⊥MN,得GM=2MN,根据∠BAC=45![]() ,BC∥AD得到AM=BF,再证△BFH≌△AMN,得到GM=2FH,
,BC∥AD得到AM=BF,再证△BFH≌△AMN,得到GM=2FH,
由此得到结论.
(1)∵![]() ,
,
∴△ABC是等腰直角三角形,
∵![]() ,
,
∴AB=AD=BC=DC,
∴四边形ABCD是菱形,
∵![]() ,
,
∴四边形ABCD是正方形,
∴∠BCD=![]() ,
,
∴∠CDE=![]() ,
,
∵BF=DE,BC=DC,
∴△BCF≌△DCE,
∴四边形![]() 的面积=S正方形ABCD=AB2=102=100.
的面积=S正方形ABCD=AB2=102=100.
(2)延长BG交AD于点M,作AN⊥MN,连接FG,
∵△BCF≌△DCE,
∴∠BCF=∠DCE,
∴∠FCE=∠BCD=![]() ,
,
∵BG⊥CF,
∴∠FHM=∠FCE=![]() ,
,
∴BM∥CE,
∵BC∥AD,
∴四边形BCEM是平行四边形,
∴BM=CE.
∵![]() ,BG⊥CF,
,BG⊥CF,
∴∠BCH=∠GCH,∠CBM=∠CGB,
∴△BCF≌△GCF,
∴BF=GF,∠FGC=∠FBC=![]() ,
,
∵∠BAC=45![]() ,
,
∴∠AFG=∠BAC=45![]() ,
,
∴FG=AG,
∵BC∥AD,
∴∠CBM=∠AMB,
∴∠AGM=∠CGB=∠CBM=∠AMB,
∴AM=AG,
∵AN⊥MN,
∴GM=2MN,
∵∠BAD=∠ANM=![]() ,
,
∴∠ABM+∠AMN=∠MAN+∠AMN=![]() ,
,
∴∠ABM=∠MAN,
∵AM=AG=FG=BF,∠BHF=∠ANM=![]() ,
,
∴△BFH≌△AMN,
∴FH=MN,
∴GM=2FH,
∵BG+GM=CE,
∴![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
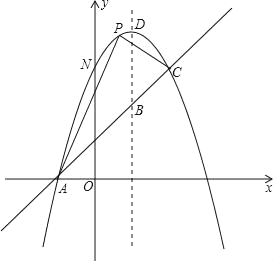
新课标快乐提优暑假作业陕西旅游出版社系列答案【题目】下表中给出了变量x,与y=ax2,y=ax2+bx+c之间的部分对应值,(表格中的符号“…”表示该项数据已丢失)
x | ﹣1 | 0 | 1 |
ax2 | … | … | 1 |
ax2+bx+c | 7 | 2 | … |
(1)求抛物线y=ax2+bx+c的表达式
(2)抛物线y=ax2+bx+c的顶点为D,与y轴的交点为A,点M是抛物线对称轴上一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求B点坐标;
(3)在(2)的条件下,设线段BD与x轴交于点C,试写出∠BAD和∠DCO的数量关系,并说明理由.