题目内容
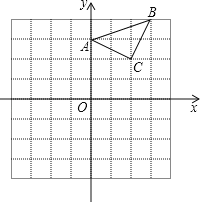
【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线![]() 经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
(1)求抛物线的解析式;
(2)点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)点E的坐标为(﹣
;(2)点E的坐标为(﹣![]() ,﹣
,﹣![]() );(3)点P的坐标为(﹣
);(3)点P的坐标为(﹣![]() ,
,![]() )或(﹣1﹣
)或(﹣1﹣![]() ,﹣
,﹣![]() )或(﹣1+
)或(﹣1+![]() ,﹣
,﹣![]() ).
).
【解析】
试题(1)首先依据等腰直角三角形的性质求得点B的坐标,然后将点A和点B的坐标代入抛物线的解析式求解即可;
(2)设直线AB的解析式为y=kx+b,将点A和点B的坐标代入可求得直线AB的解析式,设点E的坐标为(t,t﹣1),则点F的坐标为(t,![]() ),然后列出EF关于t的函数关系式,最后利用配方法求得EF的最大值即可;
),然后列出EF关于t的函数关系式,最后利用配方法求得EF的最大值即可;
(3)过点F作直线a⊥EF,交抛物线与点P,过点E作直线b⊥EF,交抛物线P′、P″,先求得点E和点F的纵坐标,然后将点E和点F的纵坐标代入抛物线的解析式求得对应的x的值,从而可求得点P、P′、P″的坐标.
试题解析:(1)∵A,C的坐标分别为(1,0),(﹣4,0),∴AC=5.∵△ABC为等腰直角三角形,∠C=90°,∴BC=AC=5,∴B(﹣4,﹣5).将点A和点B的坐标代入得:![]() ,解得:
,解得:![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
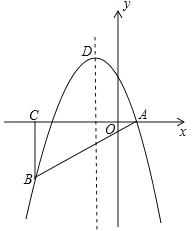
(2)如图1所示:

设直线AB的解析式为y=kx+b,将点A和点B的坐标代入得:![]() ,解得:k=1,b=﹣1.
,解得:k=1,b=﹣1.
所以直线AB的解析式为y=x﹣1.设点E的坐标为(t,t﹣1),则点F的坐标为(t,![]() ),∴EF=
),∴EF=![]() ﹣(t﹣1)=
﹣(t﹣1)=![]() =
=![]() ,∴当t=﹣
,∴当t=﹣![]() 时,FE取最大值
时,FE取最大值![]() ,此时,点E的坐标为(﹣
,此时,点E的坐标为(﹣![]() ,﹣
,﹣![]() ).
).
(3)存在点P,能使△PEF是以EF为直角边的直角三角形.理由:如图所示:过点F作直线a⊥EF,交抛物线与点P,过点E作直线b⊥EF,交抛物线P′、P″.

由(2)可知点E的坐标为(t,t﹣1),则点F的坐标为(t,![]() ),t=﹣
),t=﹣![]() ,∴点E(﹣
,∴点E(﹣![]() ,﹣
,﹣![]() )、F(﹣
)、F(﹣![]() ,
,![]() ).
).
①当![]() =
=![]() 时,解得:x=﹣
时,解得:x=﹣![]() 或x=﹣
或x=﹣![]() (舍去),∴点P的坐标为(﹣
(舍去),∴点P的坐标为(﹣![]() ,
,![]() ).
).
②当![]() =﹣
=﹣![]() 时,解得:x=﹣1+
时,解得:x=﹣1+![]() 或x=﹣1﹣
或x=﹣1﹣![]() ,∴点P′(﹣1﹣
,∴点P′(﹣1﹣![]() ,﹣
,﹣![]() ),P″(﹣1+
),P″(﹣1+![]() ,﹣
,﹣![]() ).
).
综上所述,点P的坐标为(﹣![]() ,
,![]() )或(﹣1﹣
)或(﹣1﹣![]() ,﹣
,﹣![]() )或(﹣1+
)或(﹣1+![]() ,﹣
,﹣![]() ).
).