题目内容
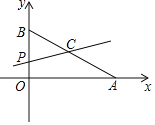
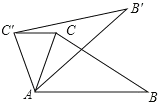
【题目】如图,△ABC各顶点坐标分别为A(4,4),B(﹣2,2),C(3,0),

①画出它的以原点O为对称中心的△A'B'C';
②在y轴上有一点P,使BP+C'P最小,求出P点坐标.
【答案】①见解析;②P点坐标为(0,![]() )
)
【解析】
①利用关于原点对称的点的坐标特征写出A′、B′、C′的坐标,然后描点即可;
②如图,BC于y轴的交点即为P点,利用两点之间线段最短得到此时BP+C′P的值最小,再利用待定系数法求出直线BC的解析式,从而得到P点坐标.
解:①如图,△A'B'C'为所作;
②如图,BC于y轴的交点即为P点,

∵C点和C′点关于y轴对称,
∴PC=PC′,
∴BP+PC′=BP+PC=BC,
∴此时BP+C′P的值最小,
设直线BC的解析式为y=kx+b,
把B(﹣2,2),C(3,0)分别代入得![]() ,解得
,解得 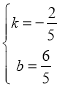 ,
,
∴直线BC的解析式为y=﹣![]() x+
x+![]() ,
,
∴P点坐标为(0,![]() ).
).

练习册系列答案
相关题目