题目内容
【题目】如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.
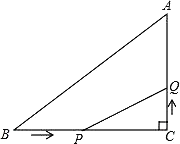
(1)若P、Q同时分别从B、C出发,那么几秒后,△PCQ的面积等于4?
(2)若P、Q同时分别从B、C出发,那么几秒后,PQ的长度等于5?
(3)△PCQ的面积何时最大,最大面积是多少?
【答案】(1)![]() 、
、![]() 秒;(2)
秒;(2)![]() 秒;(3)当t=
秒;(3)当t=![]() 时△PCQ的面积最大,最大面积为
时△PCQ的面积最大,最大面积为![]() .
.
【解析】
试题分析:(1)分别表示出线段CP和线段CQ的长,利用三角形的面积公式列出方程求解即可;
(2)表示出线段CP和CQ后利用勾股定理列出方程求解即可;
(3)列出△PCQ的面积关于t的函数解析式,配方可得最大值.
试题解析:(1)设t秒后△PCQ的面积等于4,根据题意得:CQ=t,BP=2t,则CP=7-2t,
![]() CQ×CP=
CQ×CP=![]() ×t(7-2t)=4,
×t(7-2t)=4,
整理,得:t1=![]() ,t2=
,t2=![]() ,
,
故若P、Q同时分别从B、C出发,那么![]() 、
、![]() 秒后,△PCQ的面积等于4;
秒后,△PCQ的面积等于4;
(2)若PQ的长度等于5,则PC2+QC2=PQ2,
即:(7-2t)2+t2=25,
整理,得:5t2-28t+24=0,
解得:t1=![]() ,t2=
,t2=![]() ,
,
∵CP=7-2t≥0,即t≤3.5,
∴t=![]() >3.5,舍去,
>3.5,舍去,
故那么![]() 秒后,PQ的长度等于5;
秒后,PQ的长度等于5;
(3)由(1)知△PCQ的面积S=![]() ×t(7-2t)=-(t-
×t(7-2t)=-(t-![]() )2+
)2+![]() ,
,
当t=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() ,
,
故当t=![]() 时△PCQ的面积最大,最大面积为
时△PCQ的面积最大,最大面积为![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目

