题目内容
【题目】动手操作题:如何能把一个三角形分成两个等腰三角形吗?
实际上,一个三角形只要具备下列三个条件之一,都可以被分成两个等腰三角形:
①一个角为90°;②一个角是另一个的2倍(第三角必须大于45°);
③一个角是另一个角的3倍.今天,我们通过作图来验证这个结论。
(1)问题1:
如图,Rt△ABC中,求画一条直线l将△ABC分成两个等腰三角形.并说明直线l与△ABC
边上的交点D的位置.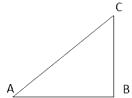
(2)问题2:
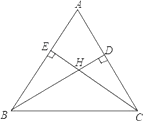
如图,△ABC中,∠ACB=80°, ∠BAC=40°,求画一条直线l把△ABC分成两个等腰三角形, 并在图中标注两个顶角的度数.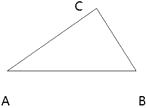
(3)问题3:
如图,△ABC中,∠ACB=120°, ∠BAC=40°,求画一条直线l把△ABC分成两个等腰三角形, 并在图中标注两个顶角的度数.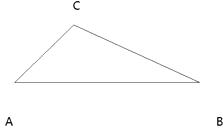
(4)问题:4:
如果等腰三角形能被一条直线分成两个等腰三角形,则原等腰三角形的顶角可以是°.(至少写出三个)
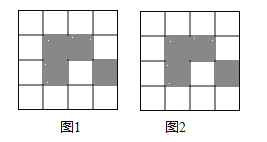
(5)拓展:已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.6条
B.7条
C.8条
D.9条
【答案】
(1)
解:点D是AC的中点

(2)
解:
(3)
解:
(4)36°,90°,108°, ![]()
(5)B
【解析】解:(4)分以下几种情况讨论:
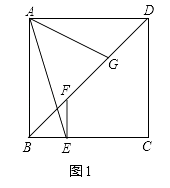
①如图1,当过顶角顶点的直线把它分成了两个等腰三角形,则AC=BC,AD=CD=BD,
图1
设![]() A=x
A=x![]() ,
,
则![]() ACD=
ACD=![]() A=x
A=x![]() ,
,![]() B=
B=![]() A=x
A=x![]() ,
,
∴![]() BCD=
BCD=![]() B=x
B=x![]() ,
,
∵![]() A+
A+![]() ACB+
ACB+![]() B=180
B=180![]() ,
,
∴x+x+x+x=180,
解得x=45,
则顶角是90![]() .
.
②如图2,若AC=BC=BD,AD=CD,
图2
设 ∠B=x ° ,
∵AC=BC,∴∠ A=∠B=x ° ,
∵AD=CD,∴∠ACD=∠A=x ° ,
∴∠BDC=∠A+∠ACD=2x ° ,
∵BC=BD, ∴∠BCD=∠BDC= 2x ° ,
∴∠ ACB=3x ° ,
∴x+x+3x=180,
解得x=36,
则顶角是108![]() .
.
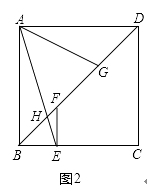
③如图3,当过底角顶点的角平分线把它分成了两个等腰三角形,则有AC=BC,AB=AD=CD,
图3
设 ∠C=x ° ,
∵AD=CD,∴∠CAD=∠C=x ° ,
∴∠ADB=∠CAD+∠C=2x ° ,
∵AD=AB,∴∠B=∠ADB=2x ° ,
∵AC =BC,∴∠CAB=∠B=2x ° ,
∵∠CAB+∠B+∠C=180 °,即2x+2x+x=180,
解得x=36,
则顶角是36![]() .
.
④如图4,当∠ A=x ° ,∠ ABC=∠ ACB=3x °时 ,也符合. AD=BD,BC=DC,
图4
∠ A=∠ ABD=x,∠ DBC=∠ BDC=2x,
则x+3x+3x=180,
解得x=![]() ,
,
则顶角是![]()
![]() .
.
综上,原等腰三角形的顶角的度数为36°,90°,108°, ![]() ,
,
所以答案是:36°,90°,108°, ![]() .
.
(5)如图所示:
当BC1=AC1 , AC=CC2,AB=BC3 , AC4=CC4 , AB=AC5 , AB=AC6 , BC7=CC7时, 都能得到符合题意的等腰三角形.
故选B.
【考点精析】利用三角形的内角和外角和直角三角形斜边上的中线对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;直角三角形斜边上的中线等于斜边的一半.