题目内容
【题目】如图,直线BD与直线BD相交得到∠1, 直线AF与直线CE相交得到∠2,点A,B,C与点D,E,F分别在同一直线上. 从①∠1=∠2 ,②∠C=∠D,③∠A=∠F三个条件中,选出两个作为已知条件,另一个作为结论组成一个问题.
(如: .从①=b,②a2=b2 两个条件中,选出一个作为已知条件,另一个作为结论可以提出两个问题:已知a=b,求证:a2=b2和已知a2=b,求证:a=b)
(1)你能提出几个问题?并把你的问题写出来.
(2)从你提出的问题中,任选一个并证明.

【答案】(1)见解析;(2)证明见解析.
【解析】分析:通过平行线的性质定理和判定定理以及对顶角的性质即可得出答案.
详解:解:(1)能提出三个问题:
已知:∠1=∠2,∠C=∠D.求证:∠A=∠F;已知:∠1=∠2,∠A=∠F.求证:∠C=∠D;已知:∠C=∠D,∠A=∠F.求证:∠1=∠2.
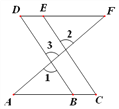
(2)解法一:已知:∠1=∠2,∠C=∠D.求证:∠A=∠F.
证明:∵∠1=∠2,∠1=∠3, ∴∠2=∠3, ∴DB∥EC,∴∠D=∠4,
∵∠C=∠D,∴∠4=∠C,∴DF∥AC, ∴∠A=∠F.
解法二:已知:∠1=∠2,∠A=∠F.求证:∠C=∠D.
证明:∵∠1=∠2,∠1=∠3, ∴∠2=∠3,∴DB∥EC,∴∠D=∠4,
∵∠A=∠F,∴DF∥AC,∴∠4=∠C, ∴∠C=∠D.
解法三:已知:∠C=∠D,∠A=∠F.求证:∠1=∠2.
∵∠A=∠F,∴DF∥AC,∴∠4=∠C, ∵∠C=∠D,∴∠4=∠D,∴DB∥EC,
∴∠2=∠3,∵∠3=∠1, ∴∠1=∠2.

【题目】某宾馆有50个房间共游客居住.当每个房间定价为180元时,房间会全部住满;当每个房间的定价增加10元时,就会有一个房间空闲.
设每个房间每天的定价增加x个10元.
(Ⅰ)填写下表:
每个房间每天定价(元) | 180 | 190 | 200 | 210 | …… | 180×10x |
住满房间个数(个) | 50 | 49 | 48 | …… |
(Ⅱ)若游客居住的房间的当天收入为y(元),写出y关于x的函数关系式;
(Ⅲ)如果游客入住房间,宾馆需对每个房间每天支出20元的各种费用.当房间定价为多少的时候,宾馆获得的利润W(元)最大?
【题目】根据下表回答问题:
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
(1)272.25的平方根是
(2)![]() = ,
= , ![]() = ,
= , ![]() =
=
(3)设![]() 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根.

