��Ŀ����
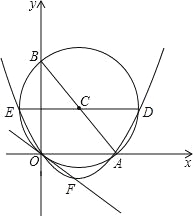
����Ŀ����ֱ������ϵ�У���C��ԭ��O����x���ڵ�A��2��0������y���ڵ�B��0��![]() ����
����
��1����Բ��C�����꣮
��2��������y=ax2+bx+c��O��A���㣬�Ҷ���������������y=-![]() ��ͼ���ϣ��������ߵĽ���ʽ��
��ͼ���ϣ��������ߵĽ���ʽ��
��3����Բ��C��ƽ����x���ֱ��DE������C��D��E���㣬���ж�D��E�����Ƿ��ڣ�2���е��������ϣ�
��4������2���е��������ϴ��ڵ�P��x0��y0����������APBΪ�۽ǣ���x0��ȡֵ��Χ��
���𰸡���1��Բ��C������Ϊ��1��![]() ����
����
��2�������ߵĽ���ʽΪy=![]() x2��
x2��![]() x��
x��
��3����D��E��������������
��4����1��x0��0����2��x0��3��
��������
�����������1����ͼ�߶�AB��ԲC��ֱ������Ϊ��A��B��������֪������ƽ���ߵ����ʼ�����õ�C�����ꣻ
��2����Ϊ�����߹���A��O�����Կ���öԳ��ᣬ���������ֱ��y=��![]() x�Ľ��㣬���Ƕ��κ����Ķ������꣬���ö���ʽ����һ��ʽ�����ô���ϵ����������������ߵĽ���ʽ��
x�Ľ��㣬���Ƕ��κ����Ķ������꣬���ö���ʽ����һ��ʽ�����ô���ϵ����������������ߵĽ���ʽ��
��3����ΪDE��x�ᣬ�ҹ���C�����Կɵ�D��E��������Ϊ![]() �����ֱ��AB�ij����ɵ�D��E�ĺ����꣬�������ʽ�����жϣ�
�����ֱ��AB�ij����ɵ�D��E�ĺ����꣬�������ʽ�����жϣ�
��4����ΪABΪֱ�������Ե��������ϵĵ�P����C���ڲ�ʱ��������APBΪ�۽ǣ����ԩ�1��x0��0����2��x0��3��
�����������1���ߡ�C����ԭ��O
��ABΪ��C��ֱ��
��CΪAB���е�
����C��CH��ֱx���ڵ�H������CH=![]() OB=
OB=![]() ��OH=
��OH=![]() OA=1
OA=1
��Բ��C������Ϊ��1��![]() ����
����
��2���������߹�O��A���㣬
�������ߵĶԳ���Ϊx=1��
�������ߵĶ�����ֱ��y=��![]() x�ϣ�
x�ϣ�
������������1����![]() ����
����
����������������������y=ax2+bx+c���� ��
��
���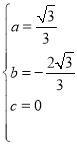 ��
��
�������ߵĽ���ʽΪy=![]() x2��
x2��![]() x��
x��
��3����OA=2��OB=2![]() ��
��
��AB=![]() =4������C�İ뾶r=2��
=4������C�İ뾶r=2��
��D��3��![]() ����E����1��
����E����1��![]() ����
����
����y=![]() x2��
x2��![]() x���飬֪��D��E�����������ϣ�
x���飬֪��D��E�����������ϣ�
��4����ABΪֱ����
�����������ϵĵ�P����C���ڲ�ʱ��������APBΪ�۽ǣ�
����1��x0��0����2��x0��3��