题目内容
如图，将三角形纸片ABC的一个角折叠，折痕为EF，若∠A=80°，∠B=68°，∠CFB=22°，则∠CEA=分析：先根据∠A=80°，∠B=68°，求出∠C的度数．再由∠CFB=22°，可求出∠CFE的度数，由三角形内角和定理及平角的性质即可求解．
解答：解：∵△ABC中，∠A=80°，∠B=68°，∴∠C=180°-∠A-∠B=180°-80°-68°=32°，
∵∠CFB=22°，∴∠CFE=
=
=79°，
在△CEF中，∠CEF=180°-∠CFE-∠C=180°-79°-32°=69°，
∴∠CEA=180°-2∠CEF=180°-2×69°=42°．
∵∠CFB=22°，∴∠CFE=
| 180°-∠CFB |
| 2 |
| 180°-22° |
| 2 |
在△CEF中，∠CEF=180°-∠CFE-∠C=180°-79°-32°=69°，
∴∠CEA=180°-2∠CEF=180°-2×69°=42°．
点评：本题考查的是三角形内角和定理，即三角形的内角和为180°．
练习册系列答案
相关题目
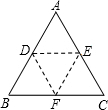如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，下列结论中，一定正确的是
如图：将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，下列结论中，一定正确的个数是（ ）
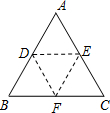
如图，将三角形纸片ABC沿DE折叠，当点A落在四边形BDEC的外部时，∠1=72°，∠2=26°，则∠A=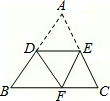
如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，下列结论中，一定正确的个数是（ ）