题目内容
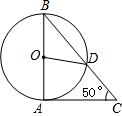
如图,AB是⊙O的直径,∠B=∠CAD.
(1)求证:AC是⊙O的切线;
(2)若点E是
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.

(1)求证:AC是⊙O的切线;
(2)若点E是
 |
| BD |

(1)∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°,
∵∠B=∠CAD,∠C=∠C,
∴△ADC∽△BAC,
∴∠BAC=∠ADC=90°,
∴BA⊥AC,
∴AC是⊙O的切线.
(2)∵BD=5,CD=4,
∴BC=9,
∵△ADC∽△BAC(已证),
∴
=
,即AC2=BC×CD=36,
解得:AC=6,
在Rt△ACD中,AD=
=2
,
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6,
∴DF=CA-CD=2,
在Rt△AFD中,AF=
=2
.
∴∠ADB=∠ADC=90°,
∵∠B=∠CAD,∠C=∠C,
∴△ADC∽△BAC,
∴∠BAC=∠ADC=90°,
∴BA⊥AC,
∴AC是⊙O的切线.
(2)∵BD=5,CD=4,
∴BC=9,
∵△ADC∽△BAC(已证),
∴
| AC |
| BC |
| CD |
| AC |
解得:AC=6,
在Rt△ACD中,AD=
| AC2-CD2 |
| 5 |
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6,
∴DF=CA-CD=2,
在Rt△AFD中,AF=
| DF2+AD2 |
| 6 |

练习册系列答案
相关题目