��Ŀ����
����Ŀ����֪����ͼֱ��l1�Ľ���ʽΪy=x+1��ֱ��l2�Ľ���ʽΪy=ax+b��a��0����������ͼ����y����һ��C��ֱ��l2��x��Ľ���B��2��0��
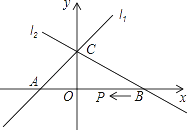
��1����a��b��ֵ��
��2��������Q��n��0���Ҵ�ֱ��x���ֱ����l1��l2�ֱ��ڵ�M��N��λ��x���Ϸ�ʱ����n��ȡֵ��Χ��
��3������P�ӵ�B������x����ÿ��1����λ�����ٶ������ƶ������ƶ�ʱ��Ϊt�룬����PACΪ����������ʱ��ֱ��д��t��ֵ��
���𰸡���1��a=��![]() ����2����1��n��2����3������������ʱ��tΪ1s��2s����3+
����2����1��n��2����3������������ʱ��tΪ1s��2s����3+![]() ����3��
����3��![]() ��s��
��s��
�����������������(1)���������������C�����꣬Ȼ��C�͵�B���������ֱ�߽���ʽ���a��b��ֵ��(2)�����������֪��Q�ڵ�A�͵�B֮�䣬�Ӷ����n��ȡֵ��Χ��(3)��������Ҫ�ּ�������ֱ������м��㣬��AC=P1C��P2A=P2C��AP3=AC��������ֱ���м���ó�t��ֵ��
���������(1)���⣺�ߵ�C��ֱ��l1��y=x+1����Ľ��㣬 ��C��0��1����
�ߵ�C��ֱ��l2�ϣ� ��b=1�� ��ֱ��l2�Ľ���ʽΪy=ax+1�� �ߵ�B��ֱ��l2�ϣ�
��2a+1=0�� ��a=��![]() ��
��
(2)���⣺�ɣ�1��֪��l1�Ľ���ʽΪy=x+1����y=0�� ��x=��1��
��ͼ��֪����Q�ڵ�A��B֮�䣬 ����1��n��2
(3)���⣺��ͼ��
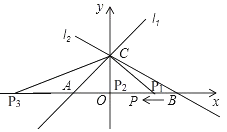
�ߡ�PAC�ǵ��������Σ� ������x����������ʱ����AC=P1Cʱ��
��CO��x�ᣬ ��OP1=OA=1�� ��BP1=OB��OP1=2��1=1�� ��1��1=1s��
����P2A=P2Cʱ����֪��P2��O�غϣ� ��BP2=OB=2�� ��2��1=2s��
����P��x�Ḻ����ʱ��AP3=AC�� ��A����1��0����C��0��1���� ��AC=![]() �� ��AP3=
�� ��AP3=![]() ��
��
��BP3=OB+OA+AP3=3+![]() ��BP3=OB+OA��AP3=3��
��BP3=OB+OA��AP3=3��![]() ��
��
����3+![]() ����1=��3+
����1=��3+![]() ��s����3��
��s����3��![]() ����1=��3��
����1=��3��![]() ��s��
��s��
��������������ʱ��tΪ1s��2s����3+![]() ����3��
����3��![]() ��s��
��s��