题目内容
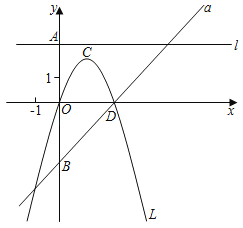
【题目】如图,若b是正数.直线l:y=b与y轴交于点A,直线a:y=x﹣b与y轴交于点B;抛物线L:y=﹣x2+bx的顶点为C,且L与x轴右交点为D.
(1)若AB=6,求b的值,并求此时L的对称轴与a的交点坐标;
(2)当点C在l下方时,求点C与l距离的最大值;
(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2019和b=2019.5时“美点”的个数.
【答案】(1)L的对称轴x=1.5,L的对称轴与a的交点为(1.5,﹣1.5 );(2)1;(3)![]() ;(4)b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.
;(4)b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.
【解析】
(1)当x=0时,y=x﹣b=﹣b,所以B (0,﹣b),而AB=6,而A(0,b),则b﹣(﹣b)=6,b=3.所以L:y=﹣x2+3x,对称轴x=1.5,当x=1.5吋,y=x﹣3=﹣1.5,于是得到结论.
(2)由y=﹣(x﹣![]() )2+
)2+![]() ,得到L的顶点C(
,得到L的顶点C(![]() ,
,![]() ),由于点C在l下方,于是得到结论;
),由于点C在l下方,于是得到结论;
(3)由題意得到y3=![]() ,即y1+y2=2y3,得b+x0﹣b=2(﹣x02+bx0)解得x0=0或x0=b﹣
,即y1+y2=2y3,得b+x0﹣b=2(﹣x02+bx0)解得x0=0或x0=b﹣![]() .但x0≠0,取x0=b﹣
.但x0≠0,取x0=b﹣![]() ,得到右交点D(b,0).于是得到结论;
,得到右交点D(b,0).于是得到结论;
(4)①当b=2019时,抛物线解析式L:y=﹣x2+2019x直线解析式a:y=x﹣2019,美点”总计4040个点,②当b=2019.5时,抛物线解析式L:y=﹣x2+2019.5x,直线解析式a:y=x﹣2019.5,“美点”共有1010个.
解:(1)当x=0时,y=x﹣b=﹣b,
∴B (0,﹣b),
∵AB=6,而A(0,b),
∴b﹣(﹣b)=6,
∴b=3.
∴L:y=﹣x2+3x,
∴L的对称轴x=1.5,
当x=1.5吋,y=x﹣3=﹣1.5,
∴L的对称轴与a的交点为(1.5,﹣1.5 );
(2)y=﹣(x﹣![]() )2+
)2+![]()
∴L的顶点C(img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/16/06e66ec6/SYS202011271613427160598622_DA/SYS202011271613427160598622_DA.002.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ),
),
∵点C在l下方,
∴C与l的距离b﹣![]() =﹣
=﹣![]() (b﹣2)2+1≤1,
(b﹣2)2+1≤1,
∴点C与1距离的最大值为1;
(3)由题意得y3=![]() ,即y1+y2=2y3,
,即y1+y2=2y3,
得b+x0﹣b=2(﹣x02+bx0)
解得x0=0或x0=b﹣![]() .但x0≠0,取x0=b﹣
.但x0≠0,取x0=b﹣![]() ,
,
对于L,当y=0吋,0=﹣x2+bx,即0=﹣x(x﹣b),
解得x1=0,x2=b,
∵b>0,
∴右交点D(b,0).
∴点(x0,0)与点D间的距离b﹣(b﹣![]() )=
)=![]() ;
;
(4)①当b=2019时,抛物线解析式L:y=﹣x2+2019x,
直线解析式a:y=x﹣2019
联立上述两个解析式可得:x1=﹣1,x2=2019,
∴可知每一个整数x的值都对应的一个整数y值,且﹣1和2019之间(包括﹣1和﹣2019)共有2021个整数;
∵另外要知道所围成的封闭图形边界分两部分:线段和抛物线,
∴线段和抛物线上各有2021个整数点,
∴总计4042个点,
∵这两段图象交点有2个点重复,
∴美点”的个数:4042﹣2=4040(个);
②当b=2019.5时,
抛物线解析式L:y=﹣x2+2019.5x,
直线解析式a:y=x﹣2019.5,
联立上述两个解析式可得:x1=﹣1,x2=2019.5,
∴当x取整数时,在一次函数y=x﹣2019.5上,y取不到整数值,因此在该图象上“美点”为0,
在二次函数y=x2+2019.5x图象上,当x为偶数时,函数值y可取整数,
可知﹣1到2019.5之 间有1010个偶数,因此“美点”共有1010个.
故b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在 点
在 点![]() 左侧),对称轴为直线
左侧),对称轴为直线![]() .
.
(1)![]() 的值为 ,在坐标系中利用描点法画出此抛物线;
的值为 ,在坐标系中利用描点法画出此抛物线;
| ··· | ··· | |||||
| ··· | ··· |
(2)若直线![]() 过点
过点![]() 且与抛物线交于点
且与抛物线交于点![]() ,请根据图象写出:当
,请根据图象写出:当![]() 时,
时,![]() 的取值范围是 .
的取值范围是 .