��Ŀ����
����Ŀ���������
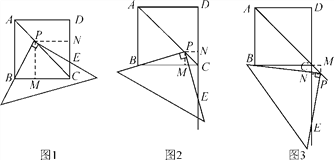
(1)��ͼ1����ֱ�����ǰ��ֱ�Ƕ���P����������ABCD�ĶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽���DC�ڵ�E���߶�PB���߶�PE�������֤����
����̽��
(2)��ͼ2���ƶ����ǰ壬ʹ���ǰ��ֱ�Ƕ���P�ڶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽�DC���ӳ����ڵ�E��(1)�еĽ��ۻ�����������������֤����������������˵�����ɣ�
������
(3)�����ƶ����ǰ壬ʹ���ǰ��ֱ�Ƕ���P�ڶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽�DC���ӳ����ڵ�E��(1)�еĽ��ۻ�����������������֤����������������˵�����ɣ�
��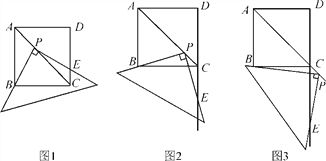
���𰸡���1��֤����������2��PB��PE������(3) PB��PE������
�������������������1�����������ε����ʵá�BCD=90�㣬ACƽ�֡�BCD����PM��CD�����ı���PMCN�Ǿ��Σ����ݽ�ƽ���ߵ����ʿɵ�PM=PN�������ı��ε��ڽǺ͵õ���PBC+��CEP=180�㣬�����õȽǵIJ�����ȵõ���PBM=��PEN��Ȼ�����AAS֤����PBM�ա�PEN�����֤����
��2������PD�����������ε����ʺͽ�ƽ���ߵ����ʣ��ɡ�SAS���Լ��ı��ε��ڽǺ͵�֤��
��3������P��PM��BC��PN��CD��Ȼ����ݽ�ƽ���ߵ����ʺ������ε����ʣ��ɡ�AAS����֤.
���������(1)��ͼ1������P��PM��BC��PN��CD������ֱ�ΪM��N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN���ߡ�BPE��90�㣬��BCD��90�㣬���PBC����CEP��180��������CEP����PEN��180�㣬���PBM����PEN������PBM����PEN�У� 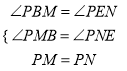 ���PBM�ա�PEN(AAS)����PB��PE��(2)��ͼ2��PB��PE���������������£�����P��PM��BC��PN��CD������ֱ�ΪM��N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN�����MPN��90�㣬�ߡ�BPE��90�㣬��BCD��90�㣬���BPM����MPE��90��������MPE����EPN��90�㣬���BPM����EPN������PBM����PEN�У�
���PBM�ա�PEN(AAS)����PB��PE��(2)��ͼ2��PB��PE���������������£�����P��PM��BC��PN��CD������ֱ�ΪM��N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN�����MPN��90�㣬�ߡ�BPE��90�㣬��BCD��90�㣬���BPM����MPE��90��������MPE����EPN��90�㣬���BPM����EPN������PBM����PEN�У� 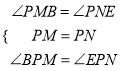 ���PBM�ա�PEN(ASA)����PB��PE��(3)��ͼ3��PB��PE���������������£�����P��PM��BC��BC���ӳ����ڵ�M��PN��CD���ӳ����ڵ�N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN�����MPN��90�㣬�ߡ�BPE��90�㣬��BCD��90�㣬���BPM����BPN��90��������BPN����EPN��90�㣬���BPM����EPN������PBM����PEN�У�
���PBM�ա�PEN(ASA)����PB��PE��(3)��ͼ3��PB��PE���������������£�����P��PM��BC��BC���ӳ����ڵ�M��PN��CD���ӳ����ڵ�N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN�����MPN��90�㣬�ߡ�BPE��90�㣬��BCD��90�㣬���BPM����BPN��90��������BPN����EPN��90�㣬���BPM����EPN������PBM����PEN�У�  ���PBM�ա�PEN(ASA)����PB��PE
���PBM�ա�PEN(ASA)����PB��PE