题目内容
【题目】如图，在长方形ABCD中，AB=6，BC=8
（1）求对角线AC的长；
（2）点E是线段CD上的一点，把△ADE沿着直线AE折叠．点D恰好落在线段AC上，点F重合，求线段DE的长．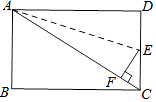 
【答案】
（1）解：在直角△ABC中，AC= 
=10；
（2）解：根据题意得AF=AD=BC=8，DE=EF，FC=AC﹣AF=10﹣8=2．
设DE=x，则EC=CD﹣DE=6﹣x，EF=DE=x．
在直角△CEF中，EF2+FC2=EC2，
则x2+4=（6﹣x）2，
解得x= 
．
【解析】（1）在直角△ABC中利用勾股定理即可求得AC的长；（2）在直角△CEF中利用勾股定理即可列方程求解．
【考点精析】认真审题，首先需要了解矩形的性质(矩形的四个角都是直角，矩形的对角线相等)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．
练习册系列答案
阅读快车系列答案
相关题目
