题目内容
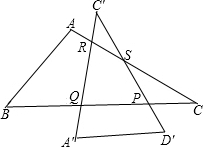
在Rt△ABC中，∠A=90°，AB=3，AC=4，以斜边BC的中点为旋转中心，把△ABC按逆时针方向旋转90°至△A′B′C′，则△ABC与△A′B′C′的重叠部分面积是______．
根据旋转的性质可知，△PSC∽△RSF∽△RQC∽△ABC，△PSC≌△QFP，
∵∠A=90°，AB=3cm，AC=4cm，
∴BC=5，PC=2.5，S△ABC=6，
∵S△PSC：S△ABC=1：4，即S△PSC=
，
∴PS=PQ=
，
∴QC=
，
∴S△RQC：S△ABC=QC2：BC2，
∴S△RQC=
，
∴SRQPS=S△RQC-S△PSC=
cm2．
故答案为
cm2．
∵∠A=90°，AB=3cm，AC=4cm，
∴BC=5，PC=2.5，S△ABC=6，
∵S△PSC：S△ABC=1：4，即S△PSC=
| 3 |
| 2 |
∴PS=PQ=
| 3 |
| 2 |
∴QC=
| 7 |
| 2 |
∴S△RQC：S△ABC=QC2：BC2，
∴S△RQC=
| 147 |
| 50 |
∴SRQPS=S△RQC-S△PSC=
| 9 |
| 4 |
故答案为
| 9 |
| 4 |
练习册系列答案
怎样学好牛津英语系列答案
相关题目
