题目内容
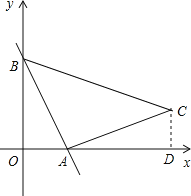
【题目】如图,一次函数 y=-2x+5 的图像分别与 x 轴,y 轴交于点A、B,以线段AB 为边在第一象限内作等腰 RtABC,BAC=90 ,求过 B、C 两点的直线的解析式.

【答案】![]()
【解析】
作CD⊥x轴于D,先确定A点坐标(![]() ,0),B点坐标(0,5),再证明△ABO≌△CAD,得到AD=OB=5,CD=OA=
,0),B点坐标(0,5),再证明△ABO≌△CAD,得到AD=OB=5,CD=OA=![]() ,则可确定C点坐标为(
,则可确定C点坐标为(![]() ,
,![]() ),然后利用待定系数法求直线BC的解析式.
),然后利用待定系数法求直线BC的解析式.
解:作CD⊥x轴于D,如图,
把y=0代入y=-2x+4得-2x+4=0,解得x=![]() ,所以A点坐标为(
,所以A点坐标为(![]() ,0),
,0),
把x=0代入y=-2x+4得y=5,所以B点坐标为(0,5),
∵△ABC为等腰直角三角形,
∴AB=AC,∠OAB+∠DAC=90°,
∴∠OBA=∠CAD,
在△ABO和△CAD中,
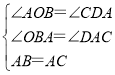
∴△ABO≌△CAD(AAS),
∴AD=OB=5,CD=OA=![]() ,
,
∴OD=OA+AD=5+![]() =
=![]() ,
,
∴C点坐标为(![]() ,
,![]() ),
),
设直线BC的解析式为y=kx+b,
把B(0,5)、C(![]() ,
,![]() )代入得
)代入得
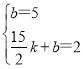 ,解得:
,解得: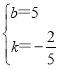 ,
,
∴直线BC的解析式为:![]() ;
;

练习册系列答案
相关题目