题目内容
【题目】已知,直线![]() ,点
,点![]() 为平面内一点,连接
为平面内一点,连接![]() 与
与![]() .
.

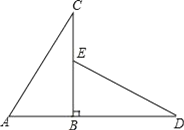
(1)如图1,点![]() 在直线
在直线![]() 、
、![]() 之间,若
之间,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
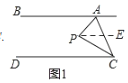
(2)如图2,点![]() 在直线
在直线![]() 、
、![]() 之间,
之间,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,写出
,写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图3,点![]() 在直线
在直线![]() 下方,
下方,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)∠APC=80°;(2)∠AKC=![]() ∠APC;(3)∠AKC=
∠APC;(3)∠AKC=![]() ∠APC.
∠APC.
【解析】
(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠APC=∠APE+∠CPE=∠BAP+∠DCP进行计算即可;
(2)过K作KE∥AB,根据KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,进而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义,得出∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)=![]() ∠APC,进而得到∠AKC=
∠APC,进而得到∠AKC=![]() ∠APC;
∠APC;
(3)过K作KE∥AB,根据KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,同理可得,∠APC=∠BAP-∠DCP,再根据角平分线的定义,得出∠BAK-∠DCK=![]() ∠BAP-
∠BAP-![]() ∠DCP=
∠DCP=![]() (∠BAP-∠DCP)=
(∠BAP-∠DCP)=![]() ∠APC,进而得到∠AKC=
∠APC,进而得到∠AKC=![]() ∠APC.
∠APC.
(1)如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;
(2)∠AKC=![]() ∠APC.
∠APC.
理由:如图2,过K作KE∥AB,

∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC=![]() ∠APC;
∠APC;
(3)∠AKC=![]() ∠APC.
∠APC.
理由:如图3,过K作KE∥AB,

∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK=∠CKE,
∴∠AKC=∠AKE∠CKE=∠BAK∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK∠DCK=![]() ∠BAP
∠BAP![]() ∠DCP=
∠DCP=![]() (∠BAP∠DCP)=
(∠BAP∠DCP)=![]() ∠APC,
∠APC,
∴∠AKC=![]() ∠APC.
∠APC.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案