题目内容
甲、乙两人同时从A地出发,沿同一条道路去B地,途中都使用两种不同的速度v1与v2(v1>v2),甲前一半的路程使用速度v1、后一半的路程使用速度v2;乙前一半的时间使用速度v2、后一半的时间使用速度v1.(1)甲、乙两人从A地到达B地的平均速度各是多少(用v1和v2表示)
(2)甲、乙两人谁先到达B地,为什么?
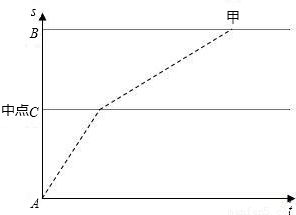
(3)如图是甲从A地到达B地的路程s与时间t的函数图象,请你在图中画出相应的乙从A地到达B地的路程s与t的函数图象.
【答案】分析:(1)设AB两地的路程为s,乙从A地到B地的总时间为a.
先算出前一半的路程所用的时间,后一半的路程所用的时间相加,速度=路程÷时间求出V甲;
先算出前一半的时间所行的路程,后一半的时间所行的路程相加,速度=路程÷时间求出V乙;
(2)看甲、乙两人谁先到达B地,因为路程一定,比较V甲,V乙的大小即可;
(3)乙从A地到达B地的路程s与t的函数图象,乙的时间短,前一半的时间的图象与甲后一半的路程的图象平行,后一半的时间的图象与甲前一半的路程的图象平行.
解答:解:V甲(1)设AB两地的路程为s,乙从A地到B地的总时间为a.
v甲= ,(3分)
,(3分)
v乙= . (3分)
. (3分)
(2)v乙-v甲=
∵0<v2<v1,
∴v乙-v甲>0,乙先到B地. (4分)
(3)如图(6分)

(只要两对平行线及三点共线即可得分)
点评:本题重点考查了实际应用和一次函数图象相结合的问题,是一道难度中等的题目.
先算出前一半的路程所用的时间,后一半的路程所用的时间相加,速度=路程÷时间求出V甲;
先算出前一半的时间所行的路程,后一半的时间所行的路程相加,速度=路程÷时间求出V乙;
(2)看甲、乙两人谁先到达B地,因为路程一定,比较V甲,V乙的大小即可;
(3)乙从A地到达B地的路程s与t的函数图象,乙的时间短,前一半的时间的图象与甲后一半的路程的图象平行,后一半的时间的图象与甲前一半的路程的图象平行.
解答:解:V甲(1)设AB两地的路程为s,乙从A地到B地的总时间为a.
v甲=
 ,(3分)
,(3分)v乙=
 . (3分)
. (3分)(2)v乙-v甲=

∵0<v2<v1,
∴v乙-v甲>0,乙先到B地. (4分)
(3)如图(6分)

(只要两对平行线及三点共线即可得分)
点评:本题重点考查了实际应用和一次函数图象相结合的问题,是一道难度中等的题目.

练习册系列答案
相关题目
甲、乙两人同时从A地出发沿同一条路线去B地,若甲一半的时间以a千米/小时的速度行走,另一半的时间以b千米/小时的速度行走;而乙一半的路程以a千米/小时的速度行走,另一半的路程以b千米/小时的速度行走(a,b均大于0且a≠b),则( )
| A、甲先到达B地 | B、乙先到达B地 | C、甲乙同时到达B地 | D、不确定 |
 乙两人同时从B地按原路返回到学校,返回时,甲和乙上、下坡的速度仍保持不变.则下列结论:
乙两人同时从B地按原路返回到学校,返回时,甲和乙上、下坡的速度仍保持不变.则下列结论: