题目内容
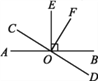
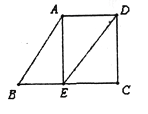
【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
【答案】(1)30°;(2)当∠EDC=30°时, AE∥DC,理由参见解析.
【解析】试题分析:(1)由已知AE⊥BC,可知∠AEC=90°,根据AB∥DE,∠B=60°,得出∠DEC=∠B= 60°(两直线平行,同位角相等),这样∠AED就求出来了;(2)此题是平行线的判定,上题已求出∠AED=30°,利用内错角相等,两直线平行,只要∠EDC=30°就可以判定AE∥DC.
试题解析:(1)∵ AB∥DE, ∴ ∠DEC=∠B= 60°(两直线平行,同位角相等),又∵ BC⊥AE,∴ ∠AEC=90°(垂直定义),所以 ∠AED=90°-60°=30°; (2)由⑴得∠AED=30°,根据内错角相等,两直线平行,∴ ∠AED=∠EDC时 AE∥DC,即当∠EDC=30°时, AE∥DC.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目