题目内容
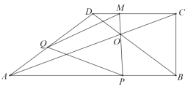
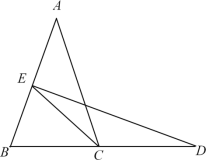
【题目】已知：如图，在△ABC中，AB=AC=6，BC=4，AB的垂直平分线交AB于点E，交BC的延长线于点D．
（1）求CD的长；
（2）求点C到ED的距离．
【答案】（1）CD=5；（2）
【解析】
（1）过A点作AF⊥BC于点F，通过等腰三角形三线合一求出BF的长度，进而求出
的值，再通过垂直平分线求出BE的长度，在Rt△DEB中利用即可求出BD的长度，进而CD的长度可求；
（2）过C点作CH⊥ED于点H，通过平行线的判定得出CH∥AB，则有
，进而可求出CH的长度，则点C到ED的距离可求．
解：（1）过A点作AF⊥BC于点F．
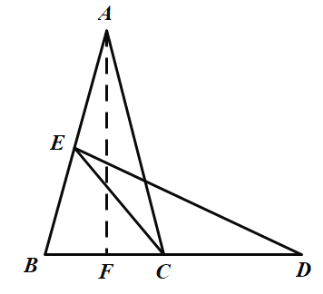
∵AB=AC=6，BC=4，AF⊥BC，
∴BF=FC=2，∠BFA=90°．
∴在Rt△ABF中，
．
∵DE垂直平分AB，AB=6，
∴AE=BE=3，∠DEB=90°．
在Rt△DEB中，
，
∴BD=9，
∴CD=BD-BC=5．
（2）过C点作CH⊥ED于点H．
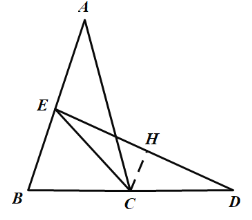
∵CH⊥ED，AB⊥ED，
∴∠DEB=∠DHC=90°，
∴CH∥AB，
∴．
∵BE=3，BD=9，CD=5，
∴
，
∴点C到ED的距离CH为．
【题目】2018年9月17日世界人工智能大会在上海召开，人工智能的变革力在教育、制造等领域加速落地. 在某市举办的一次中学生机器人足球赛中，有四个代表队进入决赛，决赛中，每个队分别与其它三个队进行主客场比赛各一场（即每个队要进行6场比赛），以下是积分表的一部分.
排名 | 代表队 | 场次 （场） | 胜 （场） | 平 （场） | 负 （场） | 净胜球 （个） | 进球 （个） | 失球 （个） | 积分 （分） |
1 | A | 6 | 1 | 6 | 12 | 6 | 22 | ||
2 | B | 6 | 3 | 2 | 1 | 0 | 6 | 6 | 19 |
3 | C | 6 | 3 | 1 | 2 | 2 | 9 | 7 | 17 |
4 | D | 6 | 0 | 0 | 6 | m | 5 | 13 | 0 |
（说明：积分＝胜场积分＋平场积分＋负场积分）
（1）D代表队的净胜球数m= ；
（2）本次决赛中，胜一场积 分，平一场积 分，负一场积 分；
（3）此次竞赛的奖金分配方案为：进入决赛的每支代表队都可以获得参赛奖金6000元；另外，在决赛期间，每胜一场可以再获得奖金2000元，每平一场再获得奖金1000元.
请根据表格提供的信息，求出冠军A队一共能获得多少奖金.
