题目内容
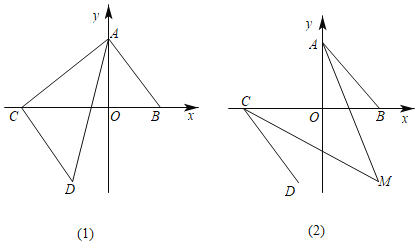
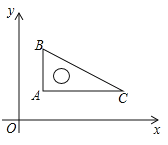
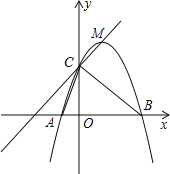
【题目】如图,二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,其中点
两点,其中点![]() ,点
,点![]() ,点
,点![]() 都在抛物线上,M为抛物线的顶点.
都在抛物线上,M为抛物线的顶点.
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 根据图形直接写出使一次函数值大于二次函数值的x的取值范围.
根据图形直接写出使一次函数值大于二次函数值的x的取值范围.
【答案】(1)![]() ;(2)15;(3)
;(2)15;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)将所A、C、D的坐标代入![]() 列出方程组,解方程组求得a、b、c的值,即可得到抛物线的解析式;
列出方程组,解方程组求得a、b、c的值,即可得到抛物线的解析式;
(2)先根据(1)中所得解析式求出点B和点M的坐标,连接OM,即可由S△MCB=S△MOC+S△MOB-S△BOC求得△MCB的面积;
(3)由图形结合点M和点C的坐标写出一次函数图象在二次函数图象上方时所对应的x的取值范围即可.
试题解析:
(1)∵二次函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() ,点
,点![]() ,
,
∴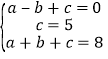 ,解得:
,解得: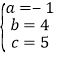 ,
,
∴该二次函数的解析式为:![]() ;
;
(2)在![]() 中,当
中,当![]() 时,有
时,有![]() ,解得:
,解得:![]() ,
,
∴点B的坐标为(5,0),
∵![]() ,
,
∴二次函数图象的顶点M的坐标为:(2,9),
如图,连接OM,BM,则:
S△BMC=S△OMC+S△OMB-S△BOC
=![]()
=15.
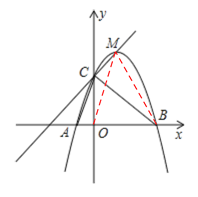
(3)由图可知在点C的左侧和点M的右侧时,一次函数的图象在二次函数图象的上方,
∴当一次函数的值大于二次函数的值时,所对应的![]() 的取值范围是:
的取值范围是:![]() 或
或![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目