Question

【题目】如图，在等腰直角△ABC中，∠ACB=90°，AC=BC，D为AB中点，DE⊥DF．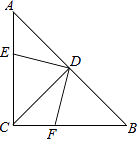
（1）写出图中所有全等三角形，分别为 ． （用“≌”符号表示）
（2）求证：ED=DF．

Answer 1

【答案】
（1）△AED≌△CFD；△CED≌△BFD；△ACD≌△BCD或△ACD≌△CBD
（2）证明：∵AC=BC，AD=BD，

∴∠CDA=90°，∠FCD=45°

∴AD=CD

∵∠CDA=∠ADE+∠EDC，

∠EDF=∠CDF+∠EDC．

∵∠EDF=∠CDA=90°，

∴∠ADE=∠CDF．

在△AED与△CFD中

，

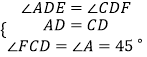∴△AED≌△CFD

∴DE=DF．

【解析】解：（1）△AED≌△CFD；△CED≌△BFD；△ACD≌△BCD或△ACD≌△CBD； 所以答案是：△AED≌△CFD；△CED≌△BFD；△ACD≌△BCD或△ACD≌△CBD；
【考点精析】认真审题，首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°)．