Question

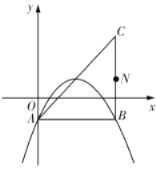
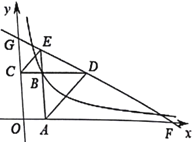
【题目】如图，矩形OABC在直角坐标系中，延长AB至点E使得BE=BC连接CE，过A作AD//CE交CB延长线于点D，直线DE分别交x轴、y轴于F、G点，若EG：DF=1：4，且△BCE与△BAD面积之和为，则过点的双曲线中的值为____．

Answer 1

【答案】3

【解析】

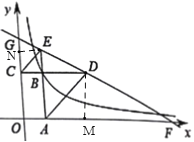
如图，过点E作EN⊥y轴于N，过点D作DM⊥x轴于M，设B（x、y），由矩形的性质及BE=BC可得△BCE是等腰直角三角形，可得∠BCE=45°，根据平行线的性质可得∠ADC=∠BCE=45°，可得△ABD是等腰直角三角形，可得BD=AB=y，根据平行线的性质可得∠NEG=∠BDE=∠MFD，可证明△NEG∽△MFD，△BDE∽△MFD，根据相似三角形的性质可得y2=4x2，根据△BCE与△BAD面积之和为可得x2+y2=，进而求出xy的值即可得答案．

如图，过点E作EN⊥y轴于N，过点D作DM⊥x轴于M，设B（x、y），

∴BC=x，AB=y，

∵BE=BC，四边形OABC是矩形，

∴△BCE是等腰直角三角形，

∴∠BCE=45°，

∵AD//CE，

∴∠ADC=∠BCE=45°，

∴△ABD是等腰直角三角形，

∴BD=AB=y，

∵EN⊥y轴，DM⊥x轴，

∴四边形GCBE、BAMD都是正方形，

∴EG=BC=x，DM=AB=y，

∵∠GNE=∠DCG=∠FOG=90°，

∴EG//CD//OF，

∴∠NEG=∠BDE=∠MFD，

∴△NEG∽△MFD，△BDE∽△MFD，

∴，，

∵，

∴，，

∴y2=4x2，

∵△BCE与△BAD面积之和为，

∴x2+y2=，即x2+y2=，

∴x2+4x2=，

解得：x2=，

∴y2=4x2=6，

∴(xy)2=9，

∵点B在双曲线图象上，且图象在第一象限，

∴k=xy=3，

故答案为：3