题目内容
【题目】(1)教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.

定理证明:请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.
定理应用:
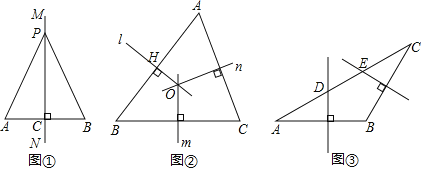
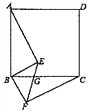
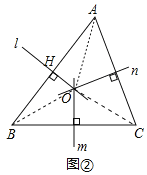
(2)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的垂直平分线,直线
的垂直平分线,直线![]() 、
、![]() 的交点为
的交点为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() .求证:
.求证:![]() .
.
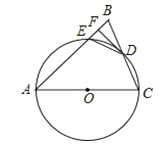
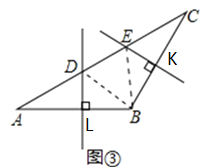
(3)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.
【答案】(1)答案见解析;(2)证明见解析;(3)5.
【解析】
(1)根据垂直得出![]() ,证明△PAC≌△PBC(SAS)即可;
,证明△PAC≌△PBC(SAS)即可;
(2)如图②中,由直线![]() 、
、![]() 的交点为
的交点为![]() ,证明出
,证明出![]() ,利用等腰三角形三线合一即可证明;
,利用等腰三角形三线合一即可证明;
(3)连接BD,BE,利用垂直平分线的性质,得出AD=BD,BE=CE,证明△BDE是等边三角形即可.
(1)如图①,定理证明:∵MN⊥AB,
∴![]()
又∵![]()
∴△PAC≌△PBC(SAS),
∴![]()
(2)连结OA、OB、OC.
∵直线m是边BC的垂直平分线,
∴![]()
∵直线n是边AC的垂直平分线,
∴![]()
∴![]()
∵OH⊥AB,
∴AH=BH.
(3)连接BD,BE,
∵∠ABC=120°,AB=AC,
∴∠A=∠C=30°,
∵直线![]() 垂直平分AB, 直线k垂直平分BC,
垂直平分AB, 直线k垂直平分BC,
∴AD=BD,BE=CE,
∴∠A=∠ABD=∠EBC=∠C=30°,
∴∠DBE=120°-30°-30°=60°,∠EDB=∠A+∠ABD=60°,
∴△BED是等边三角形,
∴AD=BD=BE=CE=DE,
∵AC=15,
∴![]() ,
,
故答案为:5.

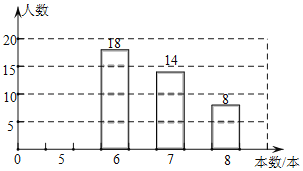
【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表:
本数(本) | 人数(人数) | 百分比 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | c | 1 |
根据以上提供的信息,解答下列问题:
(1)a=_____,b=_____,c=______;
(2)补全上面的条形统计图;
(3)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的有多少名?