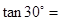题目内容
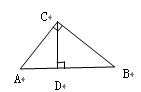
如图,在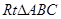 中,
中,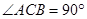 ,
,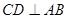 ,垂足为
,垂足为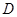 ,如果
,如果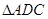 和
和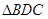 的周长之比是
的周长之比是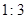 ,则
,则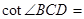 ▲ .
▲ .
 中,
中,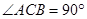 ,
,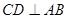 ,垂足为
,垂足为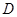 ,如果
,如果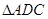 和
和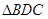 的周长之比是
的周长之比是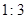 ,则
,则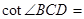 ▲ .
▲ .
根据直角三角形的直角的关系可以推出∠BCD=∠A,然后根据锐角三角函数的定义用BD表示CD,用BC表示AC,用CD表示AD,然后根据△ADC和△BDC的周长的比列式即可求解.
解:∵CD⊥AB,
∴∠A+∠ACD=90°,
∵∠ACB=∠BCD+∠ACD=90°,
∴∠BCD=∠A,
∴CD=BD?cot∠BCD,
AC=BC?cot∠A,
AD=CD?cot∠A,
∴△ADC和△BDC的周长的比为
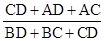 =
=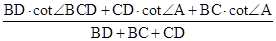
=cot∠BCD,
∵△ADC和△BDC的周长之比是1:3,
∴cot∠BCD=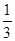 .
.
故答案为: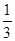 .
.
解:∵CD⊥AB,
∴∠A+∠ACD=90°,
∵∠ACB=∠BCD+∠ACD=90°,
∴∠BCD=∠A,
∴CD=BD?cot∠BCD,
AC=BC?cot∠A,
AD=CD?cot∠A,
∴△ADC和△BDC的周长的比为
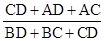 =
=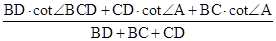
=cot∠BCD,
∵△ADC和△BDC的周长之比是1:3,
∴cot∠BCD=
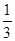 .
.故答案为:
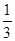 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的高,站在点
的高,站在点 处,看建筑物的顶端
处,看建筑物的顶端 ,测得仰角为
,测得仰角为 ,再往建筑物方向
,再往建筑物方向 前行
前行 米到达点
米到达点 处,看到其顶端
处,看到其顶端 ,求建筑物
,求建筑物 ,
, ).
).
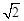 ≈l.414,
≈l.414,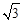 ≈1.732)
≈1.732)
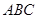 中,∠
中,∠ =90°,sin
=90°,sin =
= ,
, =15,求△
=15,求△
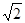 ≈1.414,
≈1.414,
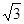 ≈1.732)(7分)
≈1.732)(7分)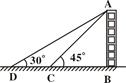
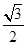 ,则∠A=__________.
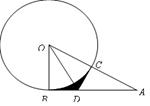
,则∠A=__________. 的切线,切点为
的切线,切点为 交
交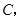 过点
过点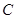 作
作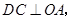 交
交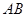 于点
于点
 ;
; 的半径为4,求CD的长;
的半径为4,求CD的长;