题目内容
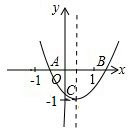已知：二次函数y=ax2+bx+c的图象如图所示，OA=OC，则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式：①| 4ac-b2 | 4a |
分析：此题可根据二次函数的性质，结合其图象可知：a＞0，-1＜c＜0，b＜0，再对各结论进行判断．
解答：解：①
=-1，抛物线顶点纵坐标为-1，正确；
②ac+b+1=0，设C（0，c），则OC=|c|，
∵OA=OC=|c|，∴A（c，0）代入抛物线得ac2+bc+c=0，又c≠0，
∴ac+b+1=0，故正确；
③abc＞0，从图象中易知a＞0，b＜0，c＜0，故正确；
④a-b+c＞0，当x=-1时y=a-b+c，由图象知（-1，a-b+c）在第二象限，
∴a-b+c＞0，故正确．
| 4ac-b2 |
| 4a |
②ac+b+1=0，设C（0，c），则OC=|c|，
∵OA=OC=|c|，∴A（c，0）代入抛物线得ac2+bc+c=0，又c≠0，
∴ac+b+1=0，故正确；
③abc＞0，从图象中易知a＞0，b＜0，c＜0，故正确；
④a-b+c＞0，当x=-1时y=a-b+c，由图象知（-1，a-b+c）在第二象限，
∴a-b+c＞0，故正确．
点评：本题考查了二次函数的性质，重点是学会由函数图象得到函数的性质．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知：二次函数的表达式为y=2x2+4x-1．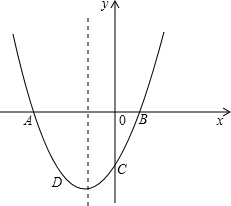
交于点C，点D（-2，-3）在抛物线上．