Question

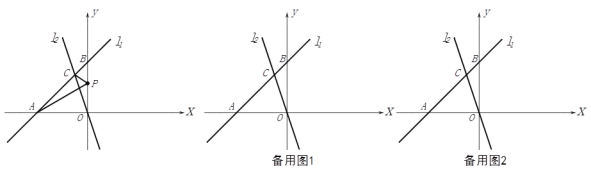
【题目】如图，在平面直角坐标系中，直线分别交轴、轴于点，直线与直线交于点,点为轴上一动点.

（1）求点的坐标；

（2）当的值最小时，求此时点的坐标，并求的最小值；

（3）在平面直角坐标系中是否存在点,使以点为顶点的四边形是平行四边形，若存在，求出点的坐标；若不存在，请说出理由.

Answer 1

【答案】（1）；（2）；（3）存在在点使以点为顶点的四边形是平行四边形；其坐标是： 或或.

【解析】

（1）联立两直线解析式组成方程组，解得即可得出结论；

（2）先确定出点A关于y轴的对称点A'，即可求出PA+PC的最小值，再用待定系数法求出直线A'C的解析式即可得出点P坐标；

（3）利用平行四边形的对角线互相平分和中点坐标公式即可得出结论.

（1）根据题意联立 解得 ∴.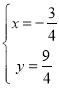

（2）如图，作点关于轴的对称点,连接交 轴于点,点就是所求作的的值最小的点，

设 所在的直线为，

由题意可列：，

解得：，

∴直线 的解析式为，

令，则，

∴，

由点可求的最小值为： ,

（3）存在点,使以点为顶点的四边形是平行四边形.

如图，作△ ,使△的三个顶点分别是其三边的中点，

设，则，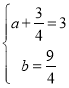

解得，

∴，

同理，

∵，

∴ 在第一、三象限的角平分线上，且，

∴ ，

综上所述，存在在点使以点为顶点的四边形是平行四边形；其坐标是：或或.