题目内容
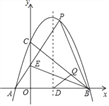
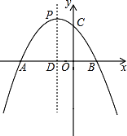
【题目】如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() )
)
(1)求m的取值范围;
(2)若OA=3OB,求抛物线的解析式;
(3)在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.
【答案】(1)m>﹣1;(2)y=﹣x2﹣2x+3;(3)存在点Q(﹣1,2)使得△BQC的周长最短.
【解析】
(1)将抛物线的问题转化到一元二次方程中,利用一元二次方程根的判别式和根与系数的关系解决;
(2)先用一元二次方程的两根表示出OA,OB,再用根与系数的关系即可;
(3)先由于点A,B关于抛物线的对称轴PD对称,连接AC与PD的交点就是使△BQC的周长最短,然后确定出直线AC解析式,最后将抛物线的对称轴代入直线AC解析式中即可.
(1)令y=0,则有﹣x2﹣2x+m+1=0,
即:x1 , x2是一元二次方程x2+2x﹣(m+1)=0,
∵抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,
∴x1x2=﹣(m+1),x1+x2=﹣2,
△=4+4(m+1)>0,
∴m>﹣2
∵x1<0,x2>0,
∴x1x2<0,
∴﹣(m+1)<0,
∴m>﹣1,
即m>﹣1
(2)解:∵A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,
∴OA=﹣x1 , OB=x2 ,
∵OA=3OB,
∴﹣x1=3x2 , ①
由(1)知,x1+x2=﹣2,②
x1x2=﹣(m+1),③
联立①②③得,x1=﹣3,x2=1,m=2,
∴抛物线的解析式y=﹣x2﹣2x+3
(3)存在点Q,
理由:如图,
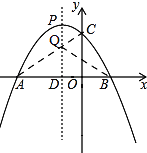
连接AC交PD于Q,点Q就是使得△BQC的周长最短,(∵点A,B关于抛物线的对称轴PD对称,)
连接BQ,
由(2)知,抛物线的解析式y=﹣x2﹣2x+3;x1=﹣3,
∴抛物线的对称轴PD为x=﹣1,C(0,3),A(﹣3,0),
∴用待定系数法得出,直线AC解析式为y=x+3,
当x=﹣1时,y=2,
∴Q(﹣1,2),
∴点Q(﹣1,2)使得△BQC的周长最短

 英才计划期末调研系列答案
英才计划期末调研系列答案