题目内容
下列给出的4个命题:
命题1 若|a|=|b|,则a|a|=b|b|;
命题2 若a2-5a+5=0,则 ;
;
命题3 若x的不等式(m+3)x>1的解集是x< ,则m<-3;
,则m<-3;
命题4 若方程x2+mx-1=0中m>0,则该方程有一正根和一负根,且负根的绝对值较大.
其中正确的命题的个数是
- A.1
- B.2
- C.3
- D.4
C
分析:命题1、代入特殊值验证正确与否;
命题2、根据求根公式求的a值,然后与1比较大小后再来解 ;
;
命题3、根据不等式的性质作答;
命题4、根据根与系数的关系解答.
解答:命题1、当a=-1,b=1时,a|a|≠b|b|;故本选项错误;
命题2、原方程的解是a=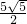 .
.
①当a= 时,1-a=-
时,1-a=- <0,所以
<0,所以 ;
;
当a= 时,1-a=-
时,1-a=-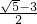 <0,所以
<0,所以 ;
;
故本选项正确;
命题3、若x的不等式(m+3)x>1的解集是x< ,则m+3<0,即m<-3,故本选项正确;
,则m+3<0,即m<-3,故本选项正确;
命题4、∵x1•x2=-1<0,
∴方程x2+mx-1=0中m>0,则该方程有一正根和一负根;
∵x1+x2=-m,且m>0,
∴-m<0,即x1+x2<0;
∴该方程有一正根和一负根,且负根的绝对值较大.
故该选项正确;
综上所述,命题2、3、4正确,共3个.
故选C.
点评:本题综合考查了根与系数的关系、绝对值、一元一次不等式及二次根式的性质与化简.都是比较基础的题目,在解得过程中只要细心一点儿就行了.
分析:命题1、代入特殊值验证正确与否;
命题2、根据求根公式求的a值,然后与1比较大小后再来解
 ;
;命题3、根据不等式的性质作答;
命题4、根据根与系数的关系解答.
解答:命题1、当a=-1,b=1时,a|a|≠b|b|;故本选项错误;
命题2、原方程的解是a=
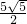 .
.①当a=
 时,1-a=-
时,1-a=- <0,所以
<0,所以 ;
;当a=
 时,1-a=-
时,1-a=-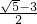 <0,所以
<0,所以 ;
;故本选项正确;
命题3、若x的不等式(m+3)x>1的解集是x<
 ,则m+3<0,即m<-3,故本选项正确;
,则m+3<0,即m<-3,故本选项正确;命题4、∵x1•x2=-1<0,
∴方程x2+mx-1=0中m>0,则该方程有一正根和一负根;
∵x1+x2=-m,且m>0,
∴-m<0,即x1+x2<0;
∴该方程有一正根和一负根,且负根的绝对值较大.
故该选项正确;
综上所述,命题2、3、4正确,共3个.
故选C.
点评:本题综合考查了根与系数的关系、绝对值、一元一次不等式及二次根式的性质与化简.都是比较基础的题目,在解得过程中只要细心一点儿就行了.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目