Question

【题目】若两个一次函数与轴的交点关于轴对称，则称这两个一次函数为“对心函数”，这两个与轴的交点为“对心点”．

（1）写出一个的对心函数：________，这两个“对心点”为：_______；

（2）直线经过点和，直线的“对心函数”直线与轴的交点位于点的上方，且直线与直线交于点，点为直线的“对心点”．点是动直线上不与重合的一个动点，且，试探究与之间的数量关系，并说明理由．

（3）如图，直线与其“对心函数”直线的交点位于第一象限，、分别为直线、的“对心点”，点为线段上一点（不含端点），连接；一动点从出发，沿线段以单位秒的速度运动到点，再沿线段以单位秒的速度运动到点后停止，点在整个运动过程中所用最短时间为秒，求直线的解析式．

Answer 1

【答案】（1）（不唯一），；；（2）详见解析；（3）

【解析】

（1）y=2x+6，令y=0，则x=-3，则这两个“对心点"为(-3，0)、(3，0)，该对心函数只要过点(3，0)即可：

（2）根据可得，

则即可求解：

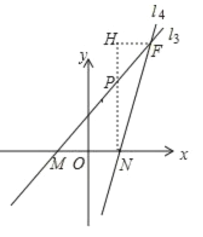
（3）过点F作x轴的平行线，过点N作y轴的平行线交l3于点P，两平行线交于点H，则此时t最小，即可求解．

（1）y=2x+6，令y=0，则x=-3

则这两个“对心点”为、；

对心点只要经过即可

例如：y=-x+3，故答案不唯一

故答案为：y=-x+3（答案不唯一）；(-3，0)、(3，0)

（2）

设，

则

故答案为：

（3）过点F作x轴的平行线，过点N作y轴的平行线l3于点P，两平行线交于点H，则此时t最小

直线l3：y=x+2，则直线的倾斜角为

∴

则PH=

=PN+PH=HN=6

故点F的纵坐标为6，则点F（4，6）

将M、F的坐标代入一次函数表达式y=kx+b

得

解得

故答案为：