题目内容
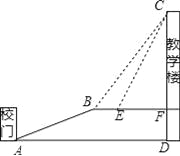
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
(1)如图1,当EF与斜边BC不相交时,试说明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF,BE,CF之间的数量关系,并说明理由;
(3)如图3,猜想EF,BE,CF之间又存在怎样的数量关系,写出猜想,说明理由.

【答案】(1)理由见解析;(2)EF=BE-CF.理由见解析.
【解析】试题分析:(1)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,从而得出答案;(2)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,根据EF=AF-AE得出答案;(3)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,根据EF=AE-AF得出答案.
试题解析:(1)因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFE=90°.
所以∠EAB+∠CAF=90°,∠EBA+∠EAB=90°.所以∠CAF=∠EBA.
在△ABE和△CAF中,∠BEA=∠AFC,∠EBA=∠FAC,AB=AC,所以△BEA≌△AFC(AAS).
所以EA=FC,BE=AF.所以EF=EA+AF=BE+CF.
(2)EF=BE-CF.理由是:因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFE=90°.
所以∠EAB+∠CAF=90°,∠ABE+∠EAB=90°.所以∠CAF=∠ABE.
在△ABE和△ACF中,∠EBA=∠FAC,∠BEA=∠CFA,AB=AC,所以△BEA≌△AFC(AAS).
所以EA=FC,BE=AF.因为EF=AF-AE,所以EF=BE-CF.
(3)EF=CF-BE.理由是:因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFA=90°.
所以∠EAB+∠CAF=90°,∠ABE+∠EAB=90°.
所以∠CAF=∠ABE.在△ABE和△ACF中,∠EBA=∠FAC,∠BEA=∠CFA,AB=AC,
所以△BEA≌△AFC(AAS).
所以EA=FC,BE=CF.因为EF=EA-AF,所以EF=CF-BE.

 阅读快车系列答案
阅读快车系列答案