题目内容
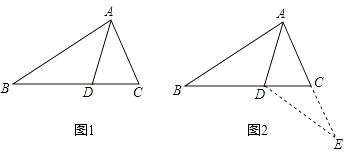
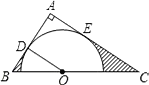
【题目】钝角三角形ABC中,∠BAC>90°,∠ACB=α,∠ABC=β,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE. 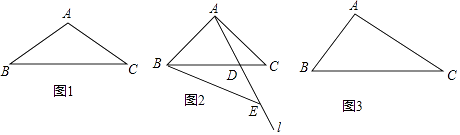
(1)若AB=AC,点E在AD延长线上. 当α=30°,点D恰好为BE中点时,补全图1,直接写出∠BAE=°,
∠BEA=°;
(2)如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
(3)如图3,若AB<AC,∠BEA的度数与(1)中②的结论相同,直接写出∠BAE,α,β满足的数量关系.
【答案】
(1)60;30
(2)解:如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N.
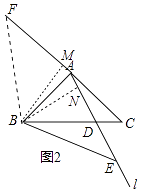
∵AB=AC,
∴∠ABC=∠C=α,
∴∠MAB=2α,∵∠BAN=2α,
∴∠BAM=∠BAN,
∴BM=BN,
在Rt△BMF和Rt△BNE中,
![]() ,
,
∴Rt△BMF≌Rt△BNE.
∴∠BEA=∠F,
∵BF=BC,
∴∠F=∠C=α,
∴∠BEA=α
(3)解:结论:∠BAE=α+β.理由如下,
如图3中,连接EC,
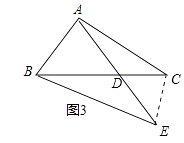
∵∠ACD=∠BED=α,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠ADB=∠CDE,
,∵∠ADB=∠CDE,
∴△ADB∽△CDE,
∴∠BAD=∠DCE,
∠ABD=∠DEC=β,
∵BC=BE,
∴∠BCE=∠BEC,
∴∠BAE=∠BEC=∠BEA+∠DEC=α+β
【解析】解:(1)补全图1,如图所示. 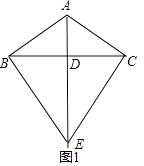
∵AB=AC,BD=DC,
∴AE⊥BC,
∴EB=EC,∠ADB=90°,
∵∠ABC=30°,
∴∠BAE=60°
∵BC=BE,
∴△BCE是等边三角形,∠DEB=∠DEC,
∴∠BEC=60°,∠BEA=30°
所以答案是60,30.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目