题目内容
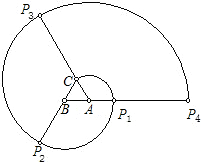
如图,正三角形ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4….设ln为扇形Dn的弧长(n=1,2,3…),回答下列问题:(1)按照要求填表:
| n | 1 | 2 | 3 | 4 |
| ln |
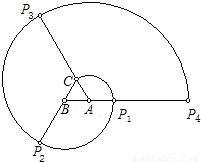
【答案】分析:从上图中可以找出规律,弧长的圆心角不变都是120度,变化的是半径,而且第一次是1,第二次是2,第三次是3,依此下去,然后按照弧长公式计算.
解答:解:(1)根据弧长公式得l1=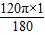 =
=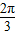 ;
;
l2=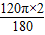 =
=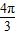 ;
;
l3=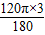 =2π;
=2π;
l4=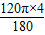 =
=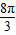 .
.
(2)根据上述规律可知:
1n=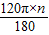 =2π×640000000,
=2π×640000000,
解得n=1.92×109.
点评:本题主要考查了弧长公式的实际应用.
解答:解:(1)根据弧长公式得l1=
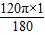 =
=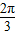 ;
;l2=
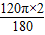 =
=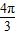 ;
;l3=
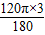 =2π;
=2π;l4=
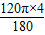 =
=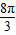 .
.| n | 1 | 2 | 3 | 4 |
| ln | 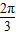 | 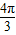 | 2π | 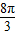 |
1n=
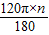 =2π×640000000,
=2π×640000000,解得n=1.92×109.
点评:本题主要考查了弧长公式的实际应用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
如图,正三角形ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4….设ln为扇形Dn的弧长(n=1,2,3…),回答下列问题:
(1)按照要求填表:
(2)根据上表所反映的规律,试估计n至少为何值时,扇形Dn的弧长能绕地球赤道一周(设地球赤道半径为6400km).
(1)按照要求填表:
| n | 1 | 2 | 3 | 4 |
| ln |

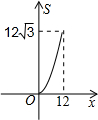
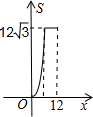
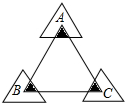 如图,正三角形ABC的边长为12,三个全等的小正三角形重心(即三条中线的交点)与正三角形ABC的顶点重合,且他们各有一边与正三角形ABC的一边平行.若小正三角形的边长为x,且0<x≤12,阴影部分的面积为S,则能反映S与x之间函数关系的大致图象是( )
如图,正三角形ABC的边长为12,三个全等的小正三角形重心(即三条中线的交点)与正三角形ABC的顶点重合,且他们各有一边与正三角形ABC的一边平行.若小正三角形的边长为x,且0<x≤12,阴影部分的面积为S,则能反映S与x之间函数关系的大致图象是( )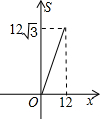
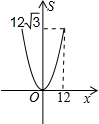
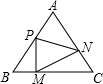 如图,正三角形ABC的边长为l,点M,N,P分别在边BC,AB上,设BM=x,CN=y,AP=z,且x+y+z=1.
如图,正三角形ABC的边长为l,点M,N,P分别在边BC,AB上,设BM=x,CN=y,AP=z,且x+y+z=1. (2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当
(2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当 如图,正三角形ABC内接于圆O,动点P在圆周的劣弧AB上,且不与A,B重合,则∠BPC=
如图,正三角形ABC内接于圆O,动点P在圆周的劣弧AB上,且不与A,B重合,则∠BPC=