题目内容
 (2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当
(2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当| 2 |
| π |
| 2 |
| 4π |
| 3 |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| 3 |
分析:首先求出S关于r的函数表达式,分析其增减性;然后根据r的取值,求出S的最大值与最小值,从而得到S的取值范围.
解答: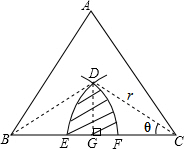 解:如右图所示,过点D作DG⊥BC于点G,易知G为BC的中点,CG=1.
解:如右图所示,过点D作DG⊥BC于点G,易知G为BC的中点,CG=1.
在Rt△CDG中,由勾股定理得:DG=
=
.
设∠DCG=θ,则由题意可得:
S=2(S扇形CDE-S△CDG)=2(
-
×1×
)=
-
,
∴S=
-
.
当r增大时,∠DCG=θ随之增大,故S随r的增大而增大.
当r=
时,DG=
=1,∵CG=1,故θ=45°,
∴S=
-
=
-1;
若r=2,则DG=
=
,∵CG=1,故θ=60°,
∴S=
-
=
-
.
∴S的取值范围是:
-1≤S<
-
.
故答案为:
-1≤S<
-
.
 解:如右图所示,过点D作DG⊥BC于点G,易知G为BC的中点,CG=1.
解:如右图所示,过点D作DG⊥BC于点G,易知G为BC的中点,CG=1.在Rt△CDG中,由勾股定理得:DG=
| CD2-CG2 |
| r2-1 |
设∠DCG=θ,则由题意可得:
S=2(S扇形CDE-S△CDG)=2(
| θπr2 |
| 360 |
| 1 |
| 2 |
| r2-1 |
| θπr2 |
| 180 |
| r2-1 |
∴S=
| θπr2 |
| 180 |
| r2-1 |
当r增大时,∠DCG=θ随之增大,故S随r的增大而增大.
当r=
| 2 |
| r2-1 |
∴S=
45π(
| ||
| 180 |
(
|
| π |
| 2 |
若r=2,则DG=
| r2-1 |
| 3 |
∴S=
| 60π22 |
| 180 |
| 22-1 |
| 4π |
| 3 |
| 3 |
∴S的取值范围是:
| π |
| 2 |
| 4π |
| 3 |
| 3 |
故答案为:
| π |
| 2 |
| 4π |
| 3 |
| 3 |
点评:本题考查扇形面积的计算、等边三角形的性质、勾股定理等重要知识点.解题关键是求出S的函数表达式,并分析其增减性.

练习册系列答案
相关题目
 (2013•十堰)如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.
(2013•十堰)如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.
 (2013•十堰)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为
(2013•十堰)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为 (2013•十堰)如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.
(2013•十堰)如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.