题目内容
【题目】去年某省将地处A,B两地的两所大学合并成了一所综合性大学,为了方便A,B两地师生的交往,学校准备在相距(1+![]() )km的A,B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东600方向、B地的西偏北450方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
)km的A,B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东600方向、B地的西偏北450方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
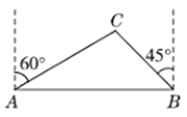
【答案】不会穿过公园;理由见解析.
【解析】
试题分析:过点C作CD⊥AB,根据题意得出BD=CD,AC=2CD,设CD=BD=x,则AC=2x,根据勾股定理得出AD=![]() x,根据AB的长度求出x的值,然后将x的值与0.7进行比较大小,得出答案.
x,根据AB的长度求出x的值,然后将x的值与0.7进行比较大小,得出答案.
试题解析:
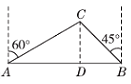
如图所示,过点C作CD⊥AB,垂足为点D. 由题意可得 ∠CAB=30°,∠CBA=45°.
在Rt△CDB中,∠BCD=45, ∴ ∠CBA=∠BCD,BD=CD.
在Rt△ACD中,∠CAB=30, ∴AC=2CD.
设CD=DB=x,则AC=2x. 由勾股定理,得 AD2=AC2CD2 AD=![]() X
X
∵ AD+DB=AB, ∴![]() +x=1+
+x=1+![]() , 解得 x=1.
, 解得 x=1.
∵CD≈1>0.7,∴计划修筑的这条公路不会穿过公园.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目