题目内容
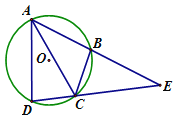
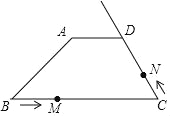
【题目】如图,在四边形ABCD中,AD∥BC,AD=3,DC=5,AB=4![]() ,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿射线CD以每秒1个单位长度的速度运动.设运动的时间为t秒.
,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿射线CD以每秒1个单位长度的速度运动.设运动的时间为t秒.
(1)BC=____.
(2)MC=_____.(用t表示)
(3)求t为何值时,四边形AMCD为平行四边形.
(4)直接写出t为何值时,△AND为直角三角形.
【答案】(1)10;(2)10﹣2t;(3)即当t=![]() 时,四边形ADCM为平行四边形;(4)t=
时,四边形ADCM为平行四边形;(4)t=![]() 或t=10时,△AND为直角三角形;
或t=10时,△AND为直角三角形;
【解析】
(1)作AE⊥BC、DF⊥BC,可得四边形AEFD为矩形,据此知AD=EF=3,根据![]() 知AE=BE=DF=4,再由
知AE=BE=DF=4,再由![]() 可得答案.
可得答案.
(2)由BM=2t、BC=10知MC=10-2t;
(3)由AD=MC即3=10-2t时,四边形ADCM为平行四边形,据此可得;
(4)①当∠AND=90°时,根据![]() 即
即
![]() 求得AN的长可得;②当∠NAD=90°时,由AD∥BC知△NAD∽△NEC,据此得
求得AN的长可得;②当∠NAD=90°时,由AD∥BC知△NAD∽△NEC,据此得![]() ,求得DN=5,据此可得答案.
,求得DN=5,据此可得答案.
(1)如图1,作AE⊥BC于点E、DF⊥BC于点F,
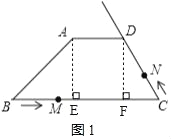
则∠AEF=∠DFC=90°,
∴AE∥DF,
∵AD∥BC,
∴四边形AEFD为矩形,
则AD=EF=3,
∵![]()
∴AE=BE=DF=4,
则FC=![]()
∴BC=BE+EF+FC=4+3+3=10,
故答案为:10;
(2)∵BM=2t,BC=10,
∴MC=10﹣2t,
故答案为:10﹣2t;
(3)∵AD∥BC,
∴当AD=MC,即3=10﹣2t时,四边形ADCM为平行四边形,
解得![]() ,
,
即当![]() 时,四边形ADCM为平行四边形;
时,四边形ADCM为平行四边形;
(4)如图2,当∠AND=90°时,

∵![]() 即
即![]()
∴AN=![]() ,
,
由CN=CD+DN可得![]()
如图3,当∠NAD=90°时,
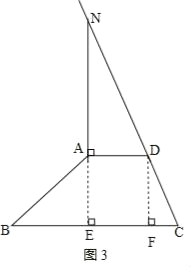
∵∠AEF=90°,AD∥BC,
∴∠EAD=90°,
∴∠NAD+∠EAD=180°,
∴点N、A、E三点共线,
∵AD∥BC,
∴△NAD∽△NEC,
∴![]() ,即
,即![]()
解得:DN=5,
∴NC=10,
∴t=10.
综上![]() 或t=10时,△AND为直角三角形.
或t=10时,△AND为直角三角形.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(1)直接写出y与x的函数关系式: .
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?