题目内容
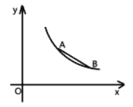
【题目】如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y=![]() 的图象上. 将线段 AB沿直线y=kx+b进行对折得到对应线段A′B′,且点A′ 始终在直线OA上,当线段A′B′ 与x轴有交点时,(1),m=____;(2),b的取值范围是____.
的图象上. 将线段 AB沿直线y=kx+b进行对折得到对应线段A′B′,且点A′ 始终在直线OA上,当线段A′B′ 与x轴有交点时,(1),m=____;(2),b的取值范围是____.
【答案】m=3 ![]() ≤b≤
≤b≤![]() .
.
【解析】
(1)由题可得m(m+1)=(m+3)(m-1),解这个方程就可求出m的值;
(2) 由于点A关于直线y=kx+b的对称点点A1始终在直线OA上,因此直线y=kx+b必与直线OA垂直,只需考虑两个临界位置(A1在x轴上、B1在x轴上)对应的b的值,就可以求出b的取值范围.
(1)∵点A(m,m+1),B(m+3,m-1)都在反比例函数y=![]() 的图象上.
的图象上.
∴m(m+1)=(m+3)(m-1).
解得:m=3.
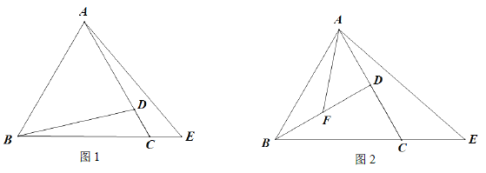
(2) ①当点B1落到x轴上时,如图1,

设直线OA的解析式为y=ax,
∵点A的坐标为(3,4),
∴3a=4,即a=![]() .
.
∴直线OA的解析式为y=![]() x.
x.
∵点A1始终在直线OA上,
∴直线y=kx+b与直线OA垂直.
∴![]() k=-1.
k=-1.
∴k=-![]() .
.
由于BB1∥OA,因此直线BB1可设为y=![]() x+c.
x+c.
∵点B的坐标为(6,2),
∴![]() ×6+c=2,即c=-6.
×6+c=2,即c=-6.
∴直线BB1解析式为y=![]() x-6.
x-6.
当y=0时,![]() x-6=0.则有x=
x-6=0.则有x=![]() .
.
∴点B1的坐标为(![]() ,0).
,0).
∵点C是BB1的中点,
∴点C的坐标为(![]() ,
,![]() )即(
)即(![]() ,1).
,1).
∵点C在直线y=-![]() x+b上,
x+b上,
∴-![]() ×
×![]() +b=1.
+b=1.
解得:b=![]() .
.
②当点A1落到x轴上时,如图2,

此时,点A1与点O重合.
∵点D是AA1的中点,A(3,4),A1(0,0),
∴D(![]() ,2).
,2).
∵点D在直线y=-![]() x+b上,
x+b上,
∴-![]() ×
×![]() +b=2.
+b=2.
解得:b=![]() .
.
综上所述:当线段A1B1与x轴有交点时,则b的取值范围为![]() ≤b≤
≤b≤![]() .
.
故答案为:![]() ≤b≤
≤b≤![]() .
.

【题目】某市篮球队到市一中选拔一名队员,教练对王亮和李刚两名同学进行![]() 次
次![]() 分投篮测试,一人每次投
分投篮测试,一人每次投![]() 个球,下图记录的是这两名同学
个球,下图记录的是这两名同学![]() 次投篮中所投中的个数.
次投篮中所投中的个数.
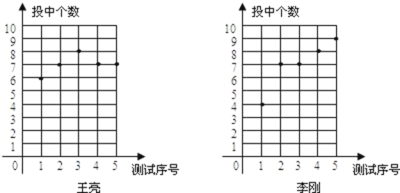
(1)请你根据图中的数据,填写下表;
姓名 | 平均数 | 众数 | 方差 |
王亮 |
| ||
李刚 |
|
|
|
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.