题目内容
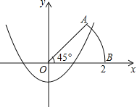
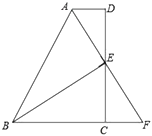
【题目】如图,在平面直角坐标系 xOy 中,直线 y ![]() x 4与 x 轴、y 轴分别交于点 A、点 B,点 D 在 y 轴的负半轴上,若将△DAB 沿着直线 AD 折叠,点 B 恰好落在 x 轴正半轴上的点 C处.
x 4与 x 轴、y 轴分别交于点 A、点 B,点 D 在 y 轴的负半轴上,若将△DAB 沿着直线 AD 折叠,点 B 恰好落在 x 轴正半轴上的点 C处.

(1)求直线 CD 的表达式;
(2)在直线 AB 上是否存在一点 P,使得 SPCD![]() SOCD?若存在,直接写出点 P 的坐标;若不存在,请说明理由.
SOCD?若存在,直接写出点 P 的坐标;若不存在,请说明理由.
【答案】(1)![]() .(2) 存在一点P为P1(
.(2) 存在一点P为P1(![]() ,
,![]() ),P2(12,-12).
),P2(12,-12).
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标,在Rt△AOB中,利用勾股定理可求出AB的长度,由折叠的性质可得出AC=AB,结合OC=OA+AC可得出OC的长度,进而可得出点C的坐标,设OD=x,则CD=DB=x+4.,Rt△OCD中,依据勾股定理可求得x的值,从而可得到点D(0,-6),然后利用待定系数法求解即可;
(2)假设存在,设点P的坐标为(m, ![]() m 4),则F(m,
m 4),则F(m, ![]() m-6),PF=
m-6),PF=![]() 利用三角形的面积公式可得出关于m的含绝对值符号的一元一次方程,解之即可得出结论.
利用三角形的面积公式可得出关于m的含绝对值符号的一元一次方程,解之即可得出结论.
解:(1)令x=0得:y=4,
∴B(0,4).
∴OB=4
令y=0得:0=-![]() x+4,解得:x=3,
x+4,解得:x=3,
∴A(3,0).
∴OA=3.
在Rt△OAB中,AB=![]() .
.
∴OC=OA+AC=3+5=8,
∴C(8,0).设OD=x,则CD=DB=x+4.
在Rt△OCD中,DC2=OD2+OC2,即(x+4)2=x2+82,解得:x=6,
∴D(0,-6).
设CD的解析式为y=kx-6,将C(8,0)代入得:8k-6=0,解得:k=![]() ,
,
∴直线CD的解析式为y=![]() x-6.
x-6.
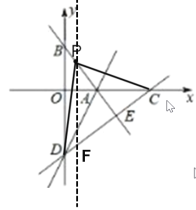
(2)过点P作PF∥y轴交CD于F, ∵P点在直线BA上,设P(m, ![]() m 4),则F(m,
m 4),则F(m, ![]() m-6), ∴PF=
m-6), ∴PF=![]() =
=![]() , ∵
, ∵![]() ,D(0,-6),C(8,0),∴
,D(0,-6),C(8,0),∴![]()
![]() ×8=
×8=![]() ×8×6×
×8×6×![]() =60,解得:m=-
=60,解得:m=-![]() 或m=12, ∴
或m=12, ∴![]() (-
(-![]() ,
,![]() ),
),![]() (12,-12),
(12,-12),
综上所述,在直线 AB 上存在一点 P为![]() (-
(-![]() ,
,![]() ),
),![]() (12,-12).
(12,-12).