题目内容
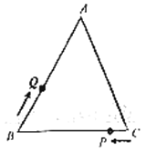
【题目】在等边![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,
的速度移动,![]() ,
,![]() 两点同时出发,它们移动的时间为
两点同时出发,它们移动的时间为![]() .
.
(1)用![]() 分别表示
分别表示![]() 及
及![]() 的长度;
的长度;
(2)经过几秒钟后,![]() 为等边三角形?
为等边三角形?
(3)若![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 两点同时出发,并且都按顺时针方向沿
两点同时出发,并且都按顺时针方向沿![]() 三边运动,请问经过几秒钟后点
三边运动,请问经过几秒钟后点![]() 与点
与点![]() 第一次在
第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
【答案】(1)![]() ;
;![]() ;(2)当
;(2)当![]() 时,
时,![]() 为等边三角形;(3)两点在
为等边三角形;(3)两点在![]() 边上第一次相遇.
边上第一次相遇.
【解析】
(1)由等边三角形的性质可求得BC的长,用t可表示出BP和BQ的长;
(2)由等边三角形的性质可知BQ=BP,可得到关于t的方程,进而可求出t的值;
(3)设经过t秒后第一次相遇,可求得t的值,进而可求得P走过的路程,确定P点的位置.
解:(1)![]() ;
;![]() ;
;
(2)若![]() 为等边三角形,则有
为等边三角形,则有![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴当![]() 时,
时,![]() 为等边三角形;
为等边三角形;
(3)设![]() 时,点
时,点![]() 与点
与点![]() 第一次相遇,
第一次相遇,
根据题意得![]() ,解得
,解得![]() ,
,
![]() 时,两点第一次相遇.
时,两点第一次相遇.
当![]() 时,
时,![]() 走过的路程为
走过的路程为![]() ,
,
而![]() ,即点
,即点![]() 此时在
此时在![]() 边上,
边上,
∴两点在![]() 边上第一次相遇.
边上第一次相遇.

练习册系列答案
相关题目