Question

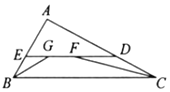
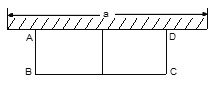
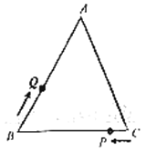
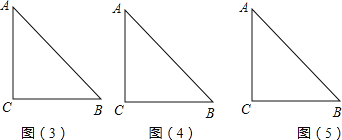
【题目】如图，形如三角板的ABC中，∠ACB=90°,∠ABC=45°,BC=12cm，形如矩形量角器的半圆O的直径DE=12cm,矩形DEFG的宽EF=6cm，矩形量角器以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在BC所在的直线上，设运动时间为x（s），矩形量角器和ABC的重叠部分的面积为S(cm2).当x=0(s)时，点E与点C重合.(图（3）、图（4）、图（5）供操作用).

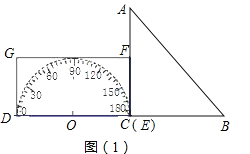
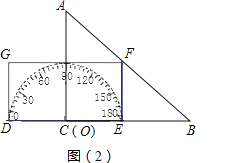
（1）当x=3时，如图（2），求S， 当x=6时，求S，当x=9时，求S；（直接写结果）

（2）当3<x<6时,求S关于x的函数关系式；

（3）当6<x<9时,求S关于x的函数关系式；

（4）当x为何值时， ABC的斜边所在的直线与半圆O所在的圆相切？

Answer 1

【答案】（1）36（cm2），54（cm2），18（cm2）；
（2）当3＜x＜6时，S=-2x2+24x-18；

（3）当6＜x＜9时，S=﹣12x+126；

（4）当x等于（9-3）秒或（9+3）秒时，△ABC的斜边所在的直线与半圆O所在的圆相切.

【解析】

（1）当x=3时，如图2根据矩形的面积公式求得S即可；当x=6时，如图3根据梯形的面积公式求得S即可；当x=9时，如图4根据三角形的面积公式求得S即可；

（2）如图5，设矩形DEFG与斜边AB的交点分别为N、H，与直角边AC的交点为M，根据S=S△ABC﹣S△AMN﹣S△BHE，将各边长用含x的式子表示，然后整理即可得到答案；

（3）如图6，设矩形DEFG与斜边AB的交点为M，延长FG交AC于点H，根据S=S△ABC﹣S△AHM﹣S矩形HCDG，将各边长用含x的式子表示，然后整理即可得到答案；

（4）如图7，图8，分两种情况，根据圆的半径长为6cm，利用勾股定理求得OB的长，即可得到x的值.

解：（1）当x=3时，CE=6cm，

如图2所示，

则S=CE·EF=6×6=36（cm2），

当x=6时，CE=12cm，

如图3所示，

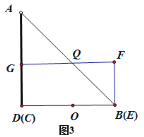
∵DG=6cm，AD=12cm，且DQ∥BC，

∴GQ是△ABC的中位线，

则S=（GQ+CE）·GD=（6+12）×6=54（cm2）；

当x=9时，CE=18cm，

如图4所示，

S=OD·GD=×6×6=18（cm2）；

故答案为：36 cm2，54 cm2，18 cm2；

（2）如图5，设矩形DEFG与斜边AB的交点分别为N、H，与直角边AC的交点为M，

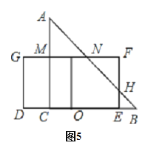
根据题意得：BE=12-2x，AM=12-6=6，

∴S=S△ABC﹣S△AMN﹣S△BHE=×12×12﹣×6×6﹣×（12-2x）2

=﹣2x2+24x-18，

故当3＜x＜6时，S=﹣2x2+24x﹣18；

（3）如图6，设矩形DEFG与斜边AB的交点为M，延长FG交AC于点H，

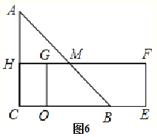
根据题意得：AH=12-6=6，HG=2x-12，

∴S=S△ABC﹣S△AHM﹣S矩形HCDG

=×12×12-×6×6-×6×（2x-12）

=﹣12x+126，

故当6＜x＜9时，S=﹣12x+126；

（4）①如图7，过点O作OD′⊥AB于点D′，

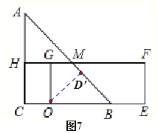
由题意得OD′=6，

∵∠ABC=45°，∠OD′B=90°，

∴OB=，

∴x==9﹣3（秒）；

②如图8，过点O作OE′⊥AB，交AB的延长线于点E′，

由题意得OE′=6，

∵∠OBE′=45°，∠OE′B=90°，

∴OB=，

∴x==9+3（秒）；

故当x等于（9﹣3）秒或（9+3）秒时，△ABC的斜边所在的直线与半圆O所在的圆相切.