题目内容
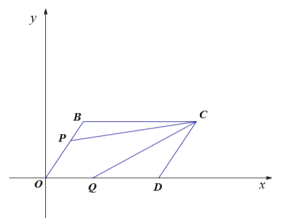
【题目】如图所示,在直角坐标系中,菱形![]() 的顶点与原点
的顶点与原点![]() 重合,
重合,![]() 与
与![]() 轴的正半轴重合,
轴的正半轴重合,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,
两点同时出发,![]() 沿
沿![]() 方向以每秒1个单位,
方向以每秒1个单位,![]() 沿
沿![]() ,
,![]() 方向以每秒2个单位运动,运动时间为
方向以每秒2个单位运动,运动时间为![]() ,当
,当![]() 运动到
运动到![]() 点时,两点同时停止运动,连接
点时,两点同时停止运动,连接![]() 、
、![]() ,请解决一下问题:
,请解决一下问题:
(1)求菱形![]() 的面积
的面积
(2)若![]() 为直角三角形,求运动时间
为直角三角形,求运动时间![]() 的值;
的值;
(3)是否存在![]() 的面积是菱形面积的
的面积是菱形面积的![]() ,若存在,求出满足条件的
,若存在,求出满足条件的![]() 的值,不存在,请说明理由
的值,不存在,请说明理由
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)由![]() ,
,![]() ,可以求出m与OB的值,菱形的高是m,利用菱形的面积
,可以求出m与OB的值,菱形的高是m,利用菱形的面积![]() ,即求出菱形的面积.
,即求出菱形的面积.
(2)分两种情况讨论,第一种情况:当![]() 时,点
时,点![]() 在
在![]() 上,则①若
上,则①若![]() ,
,![]() 时,
时,![]() ;②若
;②若![]() ,
,![]() 时,
时,![]() ;第二种情况:当
;第二种情况:当![]() 时,点
时,点![]() 在
在![]() 上,不存在
上,不存在![]() 为直角三角形.
为直角三角形.
(3)分两种情况讨论,第一种情况:当![]() 时,点
时,点![]() 在
在![]() 上
上![]() ,即是
,即是![]() ,此方程无解,所以不存在;第二种情况:当
,此方程无解,所以不存在;第二种情况:当![]() 时,点
时,点![]() 在
在![]() 上,
上,![]() 把菱形分割成两个面积相等的梯形,所以
把菱形分割成两个面积相等的梯形,所以![]() ,即
,即![]() ,由此求解即可.
,由此求解即可.
(1)∵在菱形![]() 中,
中,![]()
∴![]()
∵点![]()
∴![]() ,
,![]()
∴菱形的面积![]()
(2)第一种情况:当![]() 时,点
时,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,
①若![]() 时,
时,![]()
即![]()
![]()
![]()
②若![]() ,
,![]()
![]()
![]()
第二种情况:当![]() 时,点
时,点![]() 在
在![]() 上,不存在
上,不存在![]() 为直角三角形
为直角三角形
综上所述,![]() 或
或![]() 时,
时,![]() 为直角三角形
为直角三角形
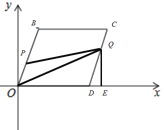
(3)如图示,第一种情况:当![]() 时,点
时,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,
![]() ,
,
即:![]()
整理得![]() ,
,
![]()
此方程无解,所以不存在;
第二种情况:当![]() 时,点
时,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,
![]() 把菱形分割成两个面积相等的梯形,
把菱形分割成两个面积相等的梯形,
∴![]()
![]()
即![]()
∴![]()
∴![]()
整理得![]()
综上所述,当![]() 时,
时,![]() 的面积是菱形面积的
的面积是菱形面积的![]() .
.

练习册系列答案
相关题目