题目内容
如图,抛物线y=x2+bx+c与x轴交于点A、B(点A在点B左侧),与y轴交于点C(0,-3),且抛物线的对称轴是直线x=1.

(1)求b的值;
(2)点E是y轴上一动点,CE的垂直平分线交y轴于点F,交抛物线于P、Q两点,且点P在第三象限.当线段PQ =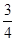 AB时,求点E的坐标;
AB时,求点E的坐标;
(3)若点M在射线CA上运动,过点M作MN⊥y轴,垂足为N,以M为圆心,MN为半径作⊙M,当⊙M与x轴相切时,求⊙M的半径.

(1)求b的值;
(2)点E是y轴上一动点,CE的垂直平分线交y轴于点F,交抛物线于P、Q两点,且点P在第三象限.当线段PQ =
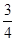 AB时,求点E的坐标;
AB时,求点E的坐标;(3)若点M在射线CA上运动,过点M作MN⊥y轴,垂足为N,以M为圆心,MN为半径作⊙M,当⊙M与x轴相切时,求⊙M的半径.
(1)b="-2" (2)点E的坐标为(0,- 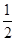 ) (3)
) (3)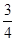
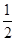 ) (3)
) (3)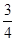
试题分析:解:(1)由图可知,对称轴x=1
X=
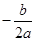 =
=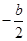 =1
=1即b=-1
(2)∵抛物线的对称轴为直线x=1
∴设抛物线的解析式为y=(x-1)2+k
∵抛物线过点C(0,-3),
∴ (0-1)2+k=-3
解得k=-4
抛物线的解析式为y=(x-1)2-4=x2-2x-3
令y=0,则x2-2x-3=0
解得x1 = 3,x2 = -1
点A坐标为(-1,0),点B坐标为(3,0)
∴AB=4,又PQ =
 AB
AB∴PQ ="3"
∵PQ⊥y轴
∴PQ∥x轴
设直线PQ交直线x=1于点G
由抛物线的轴对称性可得,PG=
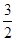
∴点P的横坐标为 -
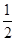
将点P的横坐标代入y=x2-2x-3中,得y =" -"
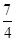
∴点P坐标为(-
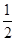 ,-
,- 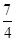 )
)∴点F坐标为(0,-
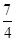 )
)∴FC=" -"
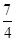 -( -3)=
-( -3)= 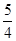
∵PQ垂直平分CE
∴CE="2" FC=
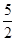
∴点E的坐标为(0,-
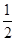 )
)(3)设直线l A C:y="k" x+ b(k≠0)
过点A(-1,0),C(0,-3)
∴y=-3x+3
∴M(xM,-3xM+3)
又∵⊙M与x轴相切,MN⊥y轴
∴x M=-3xM+3
∴x M=
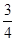
∴⊙M的半径为
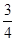
点评:此类题可以利用抛物线的对称性可求出抛物线的解析式,函数值,两点间的距离,点的坐标,利用对称点的坐标也可以求出其对称轴,要认真体会,灵活应用。

练习册系列答案
相关题目
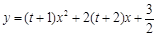 在
在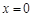 和
和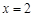 时的函数值相等。
时的函数值相等。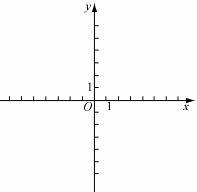
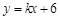 的图象与二次函数的图象都经过点
的图象与二次函数的图象都经过点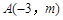 ,求
,求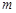 和
和 的值;
的值;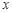 轴交于点
轴交于点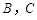 (点
(点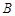 在点
在点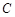 的左侧),将二次函数的图象在点
的左侧),将二次函数的图象在点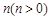 个单位后得到的图象记为
个单位后得到的图象记为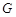 ,同时将(2)中得到的直线
,同时将(2)中得到的直线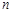 个单位。请结合图象回答:当平移后的直线与图象
个单位。请结合图象回答:当平移后的直线与图象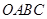 在平面直角坐标系中的位置如图所示,
在平面直角坐标系中的位置如图所示,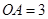 ,
,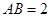 .抛物线
.抛物线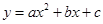 (
(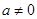 )经过点
)经过点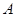 和点
和点 ,与
,与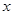 轴分别交于点
轴分别交于点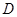 、
、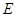 (点
(点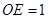 ,则下列结论:①
,则下列结论:①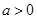 ;②
;②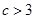 ;③
;③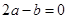 ;④
;④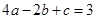 ;⑤连接
;⑤连接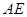 、
、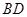 ,则
,则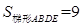 ,其中正确结论的个数为
,其中正确结论的个数为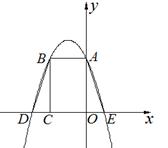
 个
个 个
个 个
个 个
个
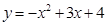 交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.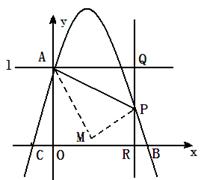
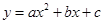 的图象中,刘敏同学观察得出了下面四条信息:
的图象中,刘敏同学观察得出了下面四条信息: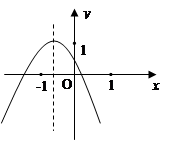
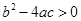 ;(2)
;(2)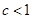 ;(3)
;(3)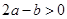 ;(4)
;(4)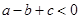 ,你认为其中错误的有( )
,你认为其中错误的有( )